
In space mission planning, scenarios that lead to mission failure, such as impact and escape for a small body orbiter, must be discovered and avoided. This problem becomes challenging if the spacecraft cannot communicate with Earth in sufficient time to make a decision, or if the dynamics of the system are unknown or uncertain, as in asteroid systems. This paper introduces a technique for automatically and intelligently exploring the reachability set of a spacecraft: the set of trajectories from a given initial condition that are possible under a specified range of control actions, so that delta-v expenditures leading to failure can be identified and avoided.
The high dimension of this problem and the nonlinear nature of gravitational interactions make reachability sets hard to compute and all but impossible to visualize. Currently, analytical approximations and heuristic reasoning about variations on known solutions are employed to plan space missions. This could both miss out on novel and improved design solutions, and also be impractical in unknown environments. The goal of this work is to automatically map out the regions that lead to failure and success. Brute-force exploration of reachability sets is computationally prohibitive, so one must focus on regions of interest: the boundaries between impact, escape, and in-system regions, known collectively as the end result regions. Doing so results in higher quality reachability sets with less error, leading to improved confidence in planning.
Reachability sets are defined from a given initial condition with a
given range of velocity impulses. If the spacecraft's engine can
deliver an impulse of up to 1 unit in any direction, for instance, the
set of possible velocity impulses forms a sphere (or disk, in 2D) of
radius 1. A naive way to explore the reachability set, then, is to
randomly choose a number of points on the delta-v surface
("exploration points"), integrate them forward in time to the mission
horizon, and determine whether the associated trajectory impacts one
of the bodies, remains in the system without impacting, or escapes the
system. The image below shows a set of trajectories in the circular
restricted three-body problem at two different timepoints in such an
exploration:

In the image below, regions of the delta-v disk are color coded
according to the outcomes of those trajectories: green and red for
impacts on each of the two bodies, blue for in-system trajectories,
and yellow for escapes. The black points are the randomly-chosen
seeds; those points are used to generate simplices that form a mesh of
the surface. Each simplex is colored according to the outcome(s) of
its vertices.
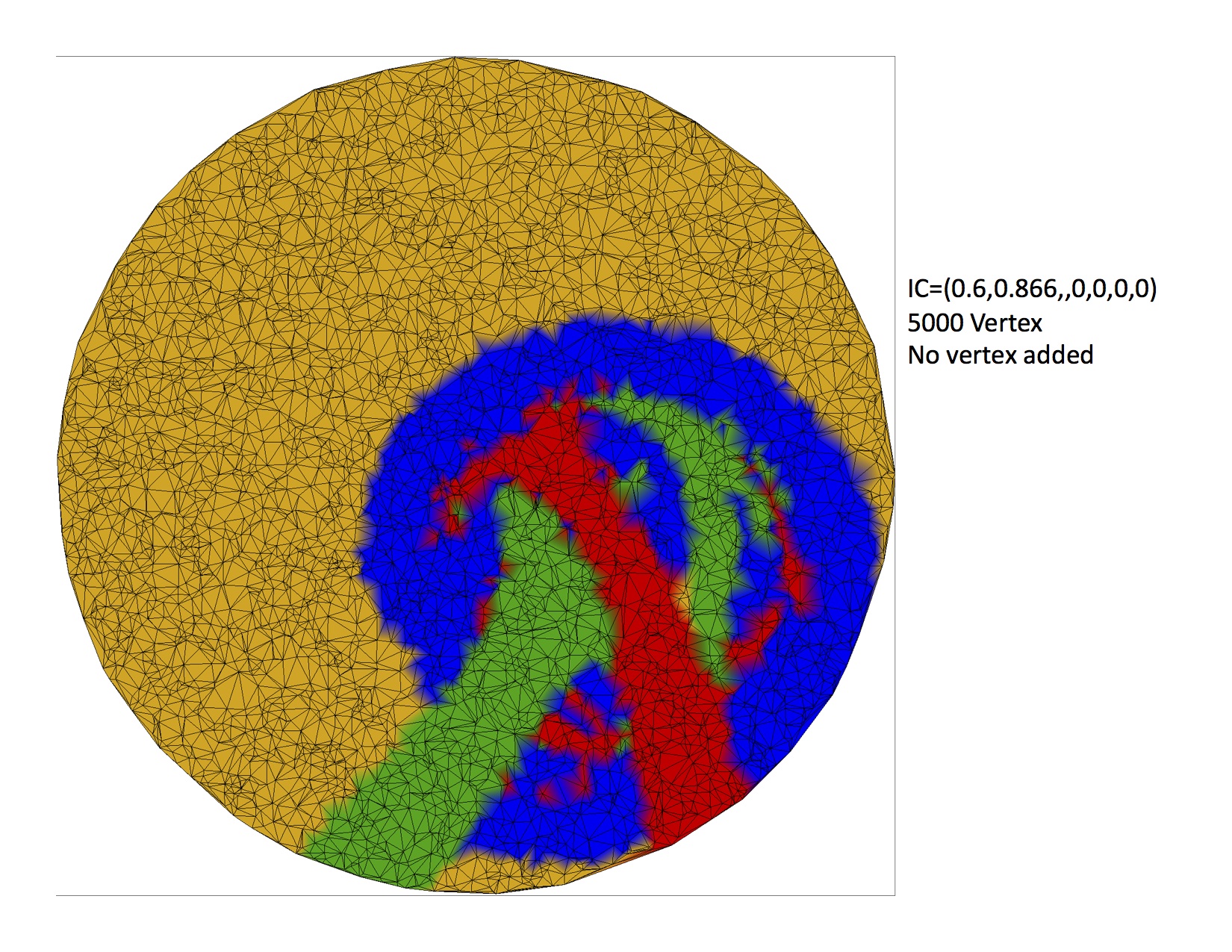
Obviously, choosing more exploration points on the initial delta-v disk will produce a finer-grained picture of the outcomes, but it will also increase the computational complexity of the process. The intellectual contribution of this project is a set of algorithms for adaptively refining the choice of exploration points in order to zero in on important regions of the reachability set while ignoring unimportant regions. This focuses the computational effort where it is most needed.
The image below shows a reachability set for the same problem as
in the image above, computed by these algorithms. The number of
vertices in the mesh is the same, but the algorithm has distributed
those vertices in a way that exposes the geometry of the region
boundaries. The refinement of the boundaries between the regions is
significant, but the computational effort of the adaptive algorithm is
only somewhat higher.

See the papers below for more information on these ideas, issues, and solutions.
View Mary Orban's
translation of this page into Slovenian (Note: we do not speak
Slovenian and cannot check the correspondence between this translation
and the material above).
