My website has moved to https://raf.prof. If you are not redirected within 2 seconds, click here.
How can one design a contract to incentivize a self-minded agent to provide honest information? What does how we measure error say about what we are trying to predict? These questions drive the area of information elicitation, which has applications to economics, machine learning, statistics, finance, engineering, and beyond. Most of the topics below fall into this broad area, such as peer prediction, prediction markets, property elicitation, and mechanism design. [Short video]
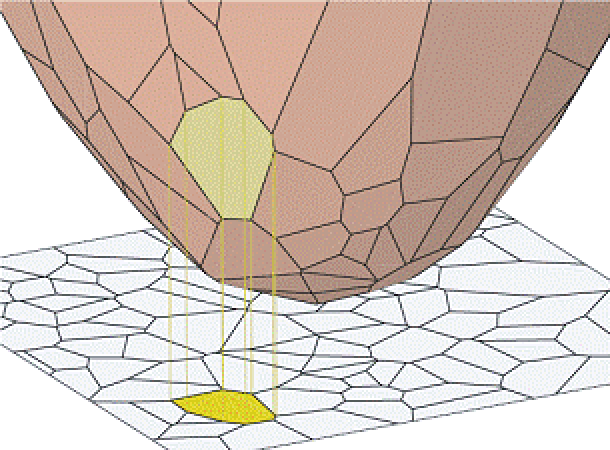
Ever since Glenn Brier sounded the warning call in 1950 that popular error measures were encouraging inaccurate meteorological forecasts, growing body of work in statistics, economics, and now computer science, has sought to design error measures which incentivize accurate forecasts. This diverse body of work goes by the name of property elicitation: the design of error measures (loss functions) that incentivize accurate statistical reports from agents or algorithms, and has applications to algorithmic economics, machine learning, finance, and engineering. My work addresses fundamental questions in this area: what statistics can be elicited (expressed as the minimizer of an expected loss function), and how many parameters are required. [Image credit: Camille Wormser] [ related papers + ]
We formalize and study the natural approach of designing convex surrogate loss functions via embeddings, for problems such as classification, ranking, or structured prediction. In this approach, one embeds each of the finitely many predictions (e.g. rankings) as a point in Rd, assigns the original loss values to these points, and "convexifies" the loss in some way to obtain a surrogate. We establish a strong connection between this approach and polyhedral (piecewise-linear convex) surrogate losses: every discrete loss is embedded by some polyhedral loss, and every polyhedral loss embeds some discrete loss. Moreover, an embedding gives rise to a consistent link function as well as linear surrogate regret bounds. Our results are constructive, as we illustrate with several examples. In particular, our framework gives succinct proofs of consistency or inconsistency for various polyhedral surrogates in the literature, and for inconsistent surrogates, it further reveals the discrete losses for which these surrogates are consistent. We go on to show additional structure of embeddings, such as the equivalence of embedding and matching Bayes risks, and the equivalence of various notions of non-redudancy. Using these results, we establish that indirect elicitation, a necessary condition for consistency, is also sufficient when working with polyhedral surrogates.
We initiate the study of proper losses for evaluating generative models in the discrete setting. Unlike traditional proper losses, we treat both the generative model and the target distribution as black-boxes, only assuming ability to draw i.i.d. samples. We define a loss to be black-box proper if the generative distribution that minimizes expected loss is equal to the target distribution. Using techniques from statistical estimation theory, we give a general construction and characterization of black-box proper losses: they must take a polynomial form, and the number of draws from the model and target distribution must exceed the degree of the polynomial. The characterization rules out a loss whose expectation is the cross-entropy between the target distribution and the model. By extending the construction to arbitrary sampling schemes such as Poisson sampling, however, we show that one can construct such a loss.
Top-k classification is a generalization of multiclass classification used widely in information retrieval, image classification, and other extreme classification settings. Several hinge-like (piecewise-linear) surrogates have been proposed for the problem, yet all are either non-convex or inconsistent. For the proposed hinge-like surrogates that are convex (i.e., polyhedral), we apply the recent embedding framework of Finocchiaro et al. (2019; 2022) to determine the prediction problem for which the surrogate is consistent. These problems can all be interpreted as variants of top-k classification, which may be better aligned with some applications. We leverage this analysis to derive constraints on the conditional label distributions under which these proposed surrogates become consistent for top-k. It has been further suggested that every convex hinge-like surrogate must be inconsistent for top-k. Yet, we use the same embedding framework to give the first consistent polyhedral surrogate for this problem.
The Lovász hinge is a convex surrogate recently proposed for structured binary classification, in which k binary predictions are made simultaneously and the error is judged by a submodular set function. Despite its wide usage in image segmentation and related problems, its consistency has remained open. We resolve this open question, showing that the Lovász hinge is inconsistent for its desired target unless the set function is modular. Leveraging a recent embedding framework, we instead derive the target loss for which the Lovász hinge is consistent. This target, which we call the structured abstain problem, allows one to abstain on any subset of the k predictions. We derive two link functions, each of which are consistent for all submodular set functions simultaneously.
We present a model of truthful elicitation which generalizes and extends mechanisms, scoring rules, and a number of related settings that do not qualify as one or the other. Our main result is a characterization theorem, yielding characterizations for all of these settings. This includes a new characterization of scoring rules for non-convex sets of distributions. We combine the characterization theorem with duality to give a simple construction to convert between scoring rules and randomized mechanisms. We also show how a generalization of this characterization gives a new proof of a mechanism design result due to Saks and Yu.
Surrogate risk minimization is an ubiquitous paradigm in supervised machine learning, wherein a target problem is solved by minimizing a surrogate loss on a dataset. Surrogate regret bounds, also called excess risk bounds, are a common tool to prove generalization rates for surrogate risk minimization. While surrogate regret bounds have been developed for certain classes of loss functions, such as proper losses, general results are relatively sparse. We provide two general results. The first gives a linear surrogate regret bound for any polyhedral (piecewise-linear convex) surrogate, meaning that surrogate generalization rates translate directly to target rates. The second shows that for sufficiently non-polyhedral surrogates, the regret bound is a square root, meaning fast surrogate generalization rates translate to slow rates for the target. Together, these results suggest polyhedral surrogates are optimal in many cases.
The convex consistency dimension of a supervised learning task is the lowest prediction dimension d such that there exists a convex surrogate L : \mathbb{R}^d \times \mathcal{Y} \to \mathbb{R} that is consistent for the given task. We present a new tool based on property elicitation, d-flats, for lower-bounding convex consistency dimension. This tool unifies approaches from a variety of domains, including continuous and discrete prediction problems. We use d-flats to obtain a new lower bound on the convex consistency dimension of risk measures, resolving an open question due to Frongillo and Kash (NeurIPS 2015). In discrete prediction settings, we show that the d-flats approach recovers and even tightens previous lower bounds using feasible subspace dimension.
We introduce a theoretical framework of elicitability and identifiability of set-valued functionals, such as quantiles, prediction intervals, and systemic risk measures. A functional is elicitable if it is the unique minimiser of an expected scoring function, and identifiable if it is the unique zero of an expected identification function; both notions are essential for forecast ranking and validation, and M- and Z-estimation. Our framework distinguishes between exhaustive forecasts, being set-valued and aiming at correctly specifying the entire functional, and selective forecasts, content with solely specifying a single point in the correct functional. We establish a mutual exclusivity result: A set-valued functional can be either selectively elicitable or exhaustively elicitable or not elicitable at all. Notably, since quantiles are well known to be selectively elicitable, they fail to be exhaustively elicitable. We further show that the class of prediction intervals and Vorob'ev quantiles turn out to be exhaustively elicitable and selectively identifiable. In particular, we provide a mixture representation of elementary exhaustive scores, leading the way to Murphy diagrams. We give possibility and impossibility results for the shortest prediction interval and prediction intervals specified by an endpoint or a midpoint. We end with a comprehensive literature review on common practice in forecast evaluation of set-valued functionals.
A property, or statistical functional, is said to be elicitable if it minimizes expected loss for some loss function. The study of which properties are elicitable sheds light on the capabilities and limitations of point estimation and empirical risk minimization. While recent work asks which properties are elicitable, we instead advocate for a more nuanced question: how many dimensions are required to indirectly elicit a given property? This number is called the elicitation complexity of the property. We lay the foundation for a general theory of elicitation complexity, including several basic results about how elicitation complexity behaves, and the complexity of standard properties of interest. Building on this foundation, our main result gives tight complexity bounds for the broad class of Bayes risks. We apply these results to several properties of interest, including variance, entropy, norms, and several classes of financial risk measures. We conclude with discussion and open directions.
One way to define the randomness of a fixed individual sequence is to ask how hard it is to predict relative to a given loss function. A sequence is memoryless if, with respect to average loss, no continuous function can predict the next entry of the sequence from a finite window of previous entries better than a constant prediction. For squared loss, memoryless sequences are known to have stochastic attributes analogous to those of truly random sequences. In this paper, we address the question of how changing the loss function changes the set of memoryless sequences, and in particular, the stochastic attributes they possess. For convex differentiable losses we establish that the statistic or property elicited by the loss determines the identity and stochastic attributes of the corresponding memoryless sequences. We generalize these results to convex non-differentiable losses, under additional assumptions, and to non-convex Bregman divergences. In particular, our results show that any Bregman divergence has the same set of memoryless sequences as squared loss. We apply our results to price calibration in prediction markets.
A common technique in supervised learning with discrete losses, such as 0-1 loss, is to optimize a convex surrogate loss over R d , calibrated with respect to the original loss. In particular, recent work has investigated embedding the original predictions (e.g. labels) as points in R^d , showing an equivalence to using polyhedral surrogates. In this work, we study the notion of the embedding dimension of a given discrete loss: the minimum dimension d such that an embedding exists. We characterize d-embeddability for all d, with a particularly tight characterization for d = 1 (embedding into the real line), and useful necessary conditions for d > 1 in the form of a quadratic feasibility program. We illustrate our results with novel lower bounds for abstain loss.
Scoring functions are commonly used to evaluate a point forecast of a particular statistical functional. This scoring function should be calibrated, meaning the correct value of the functional is the Bayes optimal forecast, in which case we say the scoring function elicits the functional. Heinrich (2014) shows that the mode functional is not elicitable. In this work, we ask whether it is at least possible to indirectly elicit the mode, wherein one elicits a low-dimensional functional from which the mode can be computed. We show that this cannot be done: neither the mode nor modal interval are indirectly elicitable with respect to the class of identifiable functionals.
We formalize and study the natural approach of designing convex surrogate loss functions via embeddings for problems such as classification or ranking. In this approach, one embeds each of the finitely many predictions (e.g. classes) as a point in Rd, assigns the original loss values to these points, and convexifies the loss in between to obtain a surrogate. We prove that this approach is equivalent, in a strong sense, to working with polyhedral (piecewise linear convex) losses. Moreover, given any polyhedral loss L, we give a construction of a link function through which $L$ is a consistent surrogate for the loss it embeds. We go on to illustrate the power of this embedding framework with succinct proofs of consistency or inconsistency of various polyhedral surrogates in the literature.
Given a data set of (x,y) pairs, a common learning task is to fit a model predicting y (a label or dependent variable) conditioned on x. This paper considers the similar but much less-understood problem of modeling "higher-order" statistics of y's distribution conditioned on x. Such statistics are often challenging to estimate using traditional empirical risk minimization (ERM) approaches. We develop and theoretically analyze an ERM-like approach with multi-observation loss functions. We propose four algorithms formalizing the concept of empirical risk minimization for this problem, two of which have statistical guarantees in settings allowing both slow and fast convergence rates, but which are out-performed empirically by the other two. Empirical results illustrate potential practicality of these algorithms in low dimensions and significant improvement over standard approaches in some settings.
Power diagrams, a type of weighted Voronoi diagrams, have many applications throughout operations research. We study the problem of power diagram detection: determining whether a given finite partition of Rd takes the form of a power diagram. This detection problem is particularly prevalent in the field of information elicitation, where one wishes to design contracts to incentivize self-minded agents to provide honest information. We devise a simple linear program to decide whether a polyhedral cell decomposition can be described as a power diagram. Further, we discuss applications to property elicitation, peer prediction, and mechanism design, where this question arises. Our model is able to efficiently decide the question for decompositions of Rd or of a restricted domain in Rd. The approach is based on the use of an alternative representation of power diagrams, and invariance of a power diagram under uniform scaling of the parameters in this representation.
A property or statistic of a distribution is said to be elicitable if it can be expressed as the minimizer of some loss function in expectation. Recent work shows that continuous real-valued properties are elicitable if and only if they are identifiable, meaning the set of distributions with the same property value can be described by linear constraints. From a practical standpoint, one may ask for which such properties do there exist convex loss functions. In this paper, in a finite-outcome setting, we show that in fact every elicitable real-valued property can be elicited by a convex loss function. Our proof is constructive, and leads to convex loss functions for new properties.
Prediction markets are well-studied in the case where predictions are probabilities or expectations of future random variables. In 2008, Lambert, et al. proposed a generalization, which we call "scoring rule markets" (SRMs), in which traders predict the value of arbitrary statistics of the random variables, provided these statistics can be elicited by a scoring rule. Surprisingly, despite active recent work on prediction markets, there has not yet been any investigation into more general SRMs. To initiate such a study, we ask the following question: in what sense are SRMs "markets"? We classify SRMs according to several axioms that capture potentially desirable qualities of a market, such as the ability to freely exchange goods (contracts) for money. Not all SRMs satisfy our axioms: once a contract is purchased in any market for prediction the median of some variable, there will not necessarily be any way to sell that contract back, even in a very weak sense. Our main result is a characterization showing that slight generalizations of cost-function-based markets are the only markets to satisfy all of our axioms for finite-outcome random variables. Nonetheless, we find that several SRMs satisfy weaker versions of our axioms, including a novel share-based market mechanism for ratios of expected values.
One way to define the "randomness" of a fixed individual sequence is to ask how hard it is to predict. When prediction error is measured via squared loss, it has been established that memoryless sequences (which are, in a precise sense, hard to predict) have some of the stochastic attributes of truly random sequences. In this paper, we ask how changing the loss function used changes the set of memoryless sequences, and in particular, the stochastic attributes they possess. We answer this question using tools from property elicitation, showing that the property elicited by the loss function determines the stochastic attributes of the corresponding memoryless sequences. We apply our results to the question of price calibration in prediction markets.
We study loss functions that measure the accuracy of a prediction based on multiple data points simultaneously. To our knowledge, such loss functions have not been studied before in the area of property elicitation or in machine learning more broadly. As compared to traditional loss functions that take only a single data point, these multi-observation loss functions can in some cases drastically reduce the dimensionality of the hypothesis required. In elicitation, this corresponds to requiring many fewer reports; in empirical risk minimization, it corresponds to algorithms on a hypothesis space of much smaller dimension. We explore some examples of the tradeoff between dimensionality and number of observations, give some geometric characterizations and intuition for relating loss functions and the properties that they elicit, and discuss some implications for both elicitation and machine-learning contexts.
The study of property elicitation is gaining ground in statistics and machine learning as a way to view and reason about the expressive power of emiprical risk minimization (ERM). Yet beyond a widening frontier of special cases, the two most fundamental questions in this area remain open: which statistics are elicitable (computable via ERM), and which loss functions elicit them? Moreover, recent work suggests a complementary line of questioning: given a statistic, how many ERM parameters are needed to compute it? We give concrete instantiations of these important questions, which have numerous applications to machine learning and related fields.
Minimal peer prediction mechanisms truthfully elicit private information (e.g., opinions or experiences) from rational agents without the requirement that ground truth is eventually revealed. In this paper, we use a geometric perspective to prove that minimal peer prediction mechanisms are equivalent to power diagrams, a type of weighted Voronoi diagram. Using this characterization and results from computational geometry, we show that many of the mechanisms in the literature are unique up to affine transformations, and introduce a general method to construct new truthful mechanisms.
Elicitation is the study of statistics or properties which are computable via empirical risk minimization. While several recent papers have approached the general question of which properties are elicitable, we suggest that this is the wrong question---all properties are elicitable by first eliciting the entire distribution or data set, and thus the important question is how elicitable. Specifically, what is the minimum number of regression parameters needed to compute the property?
Building on previous work, we introduce a new notion of elicitation complexity and lay the foundations for a calculus of elicitation. We establish several general results and techniques for proving upper and lower bounds on elicitation complexity. These results provide tight bounds for eliciting the Bayes risk of any loss, a large class of properties which includes spectral risk measures and several new properties of interest.
The elicitation of a statistic, or property of a distribution, is the task of devising proper scoring rules, equivalently proper losses, which incentivize an agent or algorithm to truthfully estimate the desired property of the underlying probability distribution.
Exploiting the connection of such elicitation to convex analysis, we address the vector-valued property case, which has received relatively little attention in the literature but is relevant for machine learning applications. We first provide a very general characterization of linear and ratio-of-linear properties, which resolves an open problem by unifying several previous characterizations in machine learning and statistics. We then ask which vectors of properties admit nonseparable scores, which cannot be expressed as a sum of scores for each coordinate separately, a natural desideratum for machine learning. We show that linear and ratio-of-linear do admit nonseparable scores, and provide evidence for the conjecture that these are the only such properties (up to link functions). Finally, we provide a general method for producing identification functions and address an open problem by showing that convex maximal level sets are insufficient for elicitability in general.
We study the problem of eliciting and aggregating probabilistic information from multiple agents. In order to successfully aggregate the predictions of agents, the principal needs to elicit some notion of confidence from agents, capturing how much experience or knowledge led to their predictions. To formalize this, we consider a principal who wishes to elicit predictions about a random variable from a group of Bayesian agents, each of whom have privately observed some independent samples of the random variable, and hopes to aggregate the predictions as if she had directly observed the samples of all agents. Leveraging techniques from Bayesian statistics, we represent confidence as the number of samples an agent has observed, which is quantified by a hyperparameter from a conjugate family of prior distributions. This then allows us to show that if the principal has access to a few samples, she can achieve her aggregation goal by eliciting predictions from agents using proper scoring rules. In particular, if she has access to one sample, she can successfully aggregate the agents' predictions if and only if every posterior predictive distribution corresponds to a unique value of the hyperparameter. Furthermore, this uniqueness holds for many common distributions of interest. When this uniqueness property does not hold, we construct a novel and intuitive mechanism where a principal with two samples can elicit and optimally aggregate the agents' predictions.
We present a model of truthful elicitation which generalizes and extends mechanisms, scoring rules, and a number of related settings that do not quite qualify as one or the other. Our main result is a characterization theorem, yielding characterizations for all of these settings, including a new characterization of scoring rules for non-convex sets of distributions. We generalize this model to eliciting some property of the agent's private information, and provide the first general characterization for this setting. We also show how this yields a new proof of a result in mechanism design due to Saks and Yu.
Ever since the Internet opened the floodgates to millions of users, each looking after their own interests, modern algorithm design has needed to be increasingly robust to strategic manipulation. Often, it is the inputs to these algorithms which are provided by strategic agents, who may lie for their own benefit, necessitating the design of algorithms which incentivize the truthful revelation of private information -- but how can this be done? This is a fundamental question with answers from many disciplines, from mechanism design to scoring rules and prediction markets. Each domain has its own model with its own assumptions, yet all seek schemes to gather private information from selfish agents, by leveraging incentives. Together, we refer to such models as elicitation.
This dissertation unifies and advances the theory of incentivized information elicitation. Using tools from convex analysis, we introduce a new model of elicitation with a matching characterization theorem which together encompass mechanism design, scoring rules, prediction markets, and other models. This lays a firm foundation on which the rest of the dissertation is built.
It is natural to consider a setting where agents report some alternate representation of their private information, called a property, rather than reporting it directly. We extend our model and characterization to this setting, revealing even deeper ties to convex analysis and convex duality, and we use these connections to prove new results for linear, smooth nonlinear, and finite-valued properties. Exploring the linear case further, we show a new four-fold equivalence between scoring rules, prediction markets, Bregman divergences, and generalized exponential families.
Applied to mechanism design, our framework offers a new perspective. By focusing on the (convex) consumer surplus function, we simplify a number of existing results, from the classic revenue equivalence theorem, to more recent characterizations of mechanism implementability.
Finally, we follow a line of research on the interpretation of prediction markets, relating a new stochastic framework to the classic Walrasian equilibrium and to stochastic mirror descent, thereby strengthening ties between prediction markets and machine learning.
We consider the design of proper scoring rules, equivalently proper losses, when the goal is to elicit some function, known as a property, of the underlying distribution. We provide a full characterization of the class of proper scoring rules when the property is linear as a function of the input distribution. A key conclusion is that any such scoring rule can be written in the form of a Bregman divergence for some convex function. We also apply our results to the design of prediction market mechanisms, showing a strong equivalence between scoring rules for linear properties and automated prediction market makers.
Markets designed for the sole purpose of gathering information from the crowd are called prediction markets. These fascinating markets have a long history dating back to markets in Rome for predicting the next pope, but modern incarnations have a very different form. I study automated market makers which are centralized agents subsidized by the market which offer to buy or sell any security, for a price which updates automatically given the history of trade. Here the central questions are how to guarantee a bounded loss for the market maker, while preserving the quality of information and adapting to market conditions and external events. [ related papers + ]
Constant-function market makers (CFMMs), such as Uniswap, are automated exchanges offering trades among a set of assets. We study their technical relationship to another class of automated market makers, cost-function prediction markets. We first introduce axioms for market makers and show that CFMMs with concave potential functions characterize "good" market makers according to these axioms. We then show that every such CFMM on n assets is equivalent to a cost-function prediction market for events with n outcomes. Our construction directly converts a CFMM into a prediction market and vice versa.
Conceptually, our results show that desirable market-making axioms are equivalent to desirable information-elicitation axioms, i.e., markets are good at facilitating trade if and only if they are good at revealing beliefs. For example, we show that every CFMM implicitly defines a proper scoring rule for eliciting beliefs; the scoring rule for Uniswap is unusual, but known. From a technical standpoint, our results show how tools for prediction markets and CFMMs can interoperate. We illustrate this interoperability by showing how liquidity strategies from both literatures transfer to the other, yielding new market designs.
One way to define the randomness of a fixed individual sequence is to ask how hard it is to predict relative to a given loss function. A sequence is memoryless if, with respect to average loss, no continuous function can predict the next entry of the sequence from a finite window of previous entries better than a constant prediction. For squared loss, memoryless sequences are known to have stochastic attributes analogous to those of truly random sequences. In this paper, we address the question of how changing the loss function changes the set of memoryless sequences, and in particular, the stochastic attributes they possess. For convex differentiable losses we establish that the statistic or property elicited by the loss determines the identity and stochastic attributes of the corresponding memoryless sequences. We generalize these results to convex non-differentiable losses, under additional assumptions, and to non-convex Bregman divergences. In particular, our results show that any Bregman divergence has the same set of memoryless sequences as squared loss. We apply our results to price calibration in prediction markets.
Prior work has investigated variations of prediction markets that preserve participants' (differential) privacy, which formed the basis of useful mechanisms for purchasing data for machine learning objectives. Such markets required potentially unlimited financial subsidy, however, making them impractical. In this work, we design an adaptively-growing prediction market with a bounded financial subsidy, while achieving privacy, incentives to produce accurate predictions, and precision in the sense that market prices are not heavily impacted by the added privacy-preserving noise. We briefly discuss how our mechanism can extend to the data-purchasing setting, and its relationship to traditional learning algorithms.
Prediction markets are well-studied in the case where predictions are probabilities or expectations of future random variables. In 2008, Lambert, et al. proposed a generalization, which we call "scoring rule markets" (SRMs), in which traders predict the value of arbitrary statistics of the random variables, provided these statistics can be elicited by a scoring rule. Surprisingly, despite active recent work on prediction markets, there has not yet been any investigation into more general SRMs. To initiate such a study, we ask the following question: in what sense are SRMs "markets"? We classify SRMs according to several axioms that capture potentially desirable qualities of a market, such as the ability to freely exchange goods (contracts) for money. Not all SRMs satisfy our axioms: once a contract is purchased in any market for prediction the median of some variable, there will not necessarily be any way to sell that contract back, even in a very weak sense. Our main result is a characterization showing that slight generalizations of cost-function-based markets are the only markets to satisfy all of our axioms for finite-outcome random variables. Nonetheless, we find that several SRMs satisfy weaker versions of our axioms, including a novel share-based market mechanism for ratios of expected values.
One way to define the "randomness" of a fixed individual sequence is to ask how hard it is to predict. When prediction error is measured via squared loss, it has been established that memoryless sequences (which are, in a precise sense, hard to predict) have some of the stochastic attributes of truly random sequences. In this paper, we ask how changing the loss function used changes the set of memoryless sequences, and in particular, the stochastic attributes they possess. We answer this question using tools from property elicitation, showing that the property elicited by the loss function determines the stochastic attributes of the corresponding memoryless sequences. We apply our results to the question of price calibration in prediction markets.
We propose a mechanism for purchasing information from a sequence of participants. The participants may simply hold data points they wish to sell, or may have more sophisticated information; either way, they are incentivized to participate as long as they believe their data points are representative or their information will improve the mechanism's future prediction on a test set. The mechanism, which draws on the principles of prediction markets, has a bounded budget and minimizes generalization error for Bregman divergence loss functions. We then show how to modify this mechanism to preserve the privacy of participants information: At any given time, the current prices and predictions of the mechanism reveal almost no information about any one participant, yet in total over all participants, information is accurately aggregated.
Prediction markets are economic mechanisms for aggregating information about future events through sequential interactions with traders. The pricing mechanisms in these markets are known to be related to optimization algorithms in machine learning and through these connections we have some understanding of how equilibrium market prices relate to the beliefs of the traders in a market. However, little is known about rates and guarantees for the convergence of these sequential mechanisms, and two recent papers cite this as an important open question.
In this paper we show how some previously studied prediction market trading models can be understood as a natural generalization of randomized coordinate descent which we call randomized subspace descent (RSD). We establish convergence rates for RSD and leverage them to prove rates for the two prediction market models above, answering the open questions. Our results extend beyond standard centralized markets to arbitrary trade networks.
In this note we elaborate on an emerging connection between three areas of research: (a) the concept of a risk measure developed within financial mathematics for reasoning about risk attitudes of agents under uncertainty, (b) the design of automated market makers for prediction markets, and (c) the family of probability distributions known as exponential families.
We study information elicitation in cost-function-based combinatorial prediction markets when the market maker’s utility for information decreases over time. In the sudden revelation setting, it is known that some piece of information will be revealed to traders, and the market maker wishes to prevent guaranteed profits for trading on the sure information. In the gradual decrease setting, the market maker’s utility for (partial) information decreases continuously over time. We design adaptive cost functions for both settings which: (1) preserve the information previously gathered in the market; (2) eliminate (or diminish) rewards to traders for the publicly revealed information; (3) leave the reward structure unaffected for other information; and (4) maintain the market maker’s worst-case loss. Our constructions utilize mixed Bregman divergence, which matches our notion of utility for information.
We introduce a framework for automated market making for prediction markets, the volume parameterized market (VPM), in which securities are priced based on the market maker's current liabilities as well as the total volume of trade in the market. We provide a set of mathematical tools that can be used to analyze markets in this framework, and show that many existing market makers (including cost-function based markets, profit-charging markets, and buy-only markets) all fall into this framework as special cases. Using the framework, we design a new market maker, the perspective market, that satisfies four desirable properties (worst-case loss, no arbitrage, increasing liquidity, and shrinking spread) in the complex market setting, but fails to satisfy information incorporation. However, we show that the sacrifice of information incorporation is unavoidable: we prove an impossibility result showing that any market maker that prices securities based only on the trade history cannot satisfy all five properties simultaneously. Instead, we show that perspective markets may satisfy a weaker notion that we call center-price information incorporation.
We strengthen recent connections between prediction markets and learning by showing that a natural class of market makers can be understood as performing stochastic mirror descent when trader demands are sequentially drawn from a fixed distribution. This provides new insights into how market prices (and price paths) may be interpreted as a summary of the market's belief distribution by relating them to the optimization problem being solved. In particular, we show that under certain conditions the stationary point of the stochastic process of prices generated by the market is equal to the market's Walrasian equilibrium of classic market analysis. Together, these results suggest how traditional market making mechanisms might be replaced with general purpose learning algorithms while still retaining guarantees about their behaviour.
We consider the design of proper scoring rules, equivalently proper losses, when the goal is to elicit some function, known as a property, of the underlying distribution. We provide a full characterization of the class of proper scoring rules when the property is linear as a function of the input distribution. A key conclusion is that any such scoring rule can be written in the form of a Bregman divergence for some convex function. We also apply our results to the design of prediction market mechanisms, showing a strong equivalence between scoring rules for linear properties and automated prediction market makers.
Machine Learning competitions such as the Netflix Prize have proven reasonably successful as a method of "crowdsourcing" prediction tasks. But these competitions have a number of weaknesses, particularly in the incentive structure they create for the participants. We propose a new approach, called a Crowdsourced Learning Mechanism, in which participants collaboratively "learn" a hypothesis for a given prediction task. The approach draws heavily from the concept of a prediction market, where traders bet on the likelihood of a future event. In our framework, the mechanism continues to publish the current hypothesis, and participants can modify this hypothesis by wagering on an update. The critical incentive property is that a participant profits exactly how much her update improves the performance of the hypothesis on a released test set.
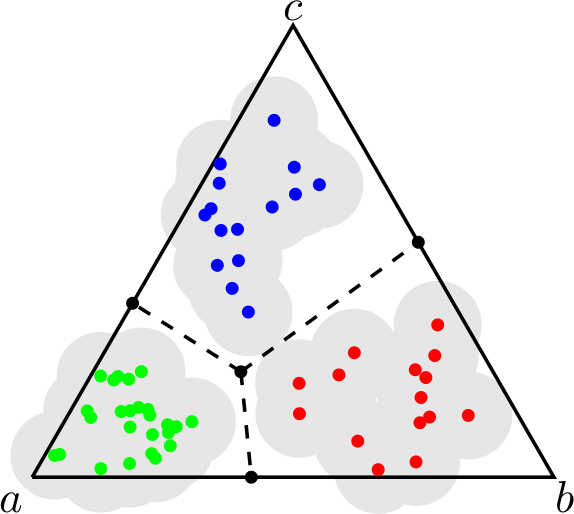
How can you incentivize someone to tell the truth if you have no way of verifying their information, and never will? This is the central question of peer prediction, whose goal is to design mechanisms that bootstrap these incentives based on several agents' responses to the same query. The field derives its name from the intuition of scoring an agent's report based on how well it "predicts" another's. Peer prediction mechanisms are notoriously brittle and unstable, and recent work has sought to understand why, and design mechanisms which are more robust. [ related papers + ]
Power diagrams, a type of weighted Voronoi diagrams, have many applications throughout operations research. We study the problem of power diagram detection: determining whether a given finite partition of Rd takes the form of a power diagram. This detection problem is particularly prevalent in the field of information elicitation, where one wishes to design contracts to incentivize self-minded agents to provide honest information. We devise a simple linear program to decide whether a polyhedral cell decomposition can be described as a power diagram. Further, we discuss applications to property elicitation, peer prediction, and mechanism design, where this question arises. Our model is able to efficiently decide the question for decompositions of Rd or of a restricted domain in Rd. The approach is based on the use of an alternative representation of power diagrams, and invariance of a power diagram under uniform scaling of the parameters in this representation.
Minimal peer prediction mechanisms truthfully elicit private information (e.g., opinions or experiences) from rational agents without the requirement that ground truth is eventually revealed. In this paper, we use a geometric perspective to prove that minimal peer prediction mechanisms are equivalent to power diagrams, a type of weighted Voronoi diagram. Using this characterization and results from computational geometry, we show that many of the mechanisms in the literature are unique up to affine transformations. We also show that classical peer prediction is "complete" in that every minimal mechanism can be written as a classical peer prediction mechanism for some scoring rule. Finally, we use our geometric characterization to develop a general method for constructing new truthful mechanisms, and we show how to optimize for the mechanisms’ effort incentives and robustness.
The problem of peer prediction is to elicit information from agents in settings without any objective ground truth against which to score reports. Peer prediction mechanisms seek to exploit correlations between signals to align incentives with truthful reports. A long-standing concern has been the possibility of uninformative equilibria. For binary signals, a multi-task output agreement (OA) mechanism due to Dasgupta and Ghosh achieves strong truthfulness, so that the truthful equilibrium strictly maximizes payoff. In this paper, we first characterize conditions on the signal distribution for which the OA mechanism remains strongly-truthful with non-binary signals. Our analysis also yields a greatly simplified proof of the earlier, binary-signal strong truthfulness result. We then introduce the multi-task CA mechanism, which extends the OA mechanism to multiple signals and provides informed truthfulness: no strategy provides more payoff in equilibrium than truthful reporting, and truthful reporting is strictly better than any uninformed strategy (where an agent avoids the effort of obtaining a signal). The CA mechanism is also maximally strongly truthful, in that no mechanism in a broader class of mechanisms is strongly truthful on more signal distributions. We then present a detail-free version of the CA mechanism that works without any knowledge requirements on the designer while retaining epsilon-informed truthfulness.
Peer prediction is the problem of eliciting private, but correlated, information from agents. By rewarding an agent for the amount that their report "predicts" that of another agent, mechanisms can promote effort and truthful reports. A common concern in peer prediction is the multiplicity of equilibria, perhaps including high-payoff equilibria that reveal no information. Rather than assume agents counterspeculate and compute an equilibrium, we adopt replicator dynamics as a model for population learning. We take the size of the basin of attraction of the truthful equilibrium as a proxy for the robustness of truthful play. We study different mechanism designs, using models estimated from real peer evaluations in several massive online courses. Among other observations, we confirm that recent mechanisms present a significant improvement in robustness over earlier approaches.
Minimal peer prediction mechanisms truthfully elicit private information (e.g., opinions or experiences) from rational agents without the requirement that ground truth is eventually revealed. In this paper, we use a geometric perspective to prove that minimal peer prediction mechanisms are equivalent to power diagrams, a type of weighted Voronoi diagram. Using this characterization and results from computational geometry, we show that many of the mechanisms in the literature are unique up to affine transformations, and introduce a general method to construct new truthful mechanisms.

In many real-world mathematical modeling applications, one eventually arrives at a complex dynamical system, a set of equations describing how the state of the system changes with time. How can we harness the ever-increasing computational power at our fingertips to make rigorous statements about these systems? For instance, one may wish to know the number of low-period orbits, or a lower bound on topological entropy. In particular, we would like a completely automated approach to producing these rigorous statements. My work in dynamics focuses on building such an approach using a combination of simple interval arithmetic to bound computational errors, and very powerful tools from computational topology, namely the discrete Conley index. [ related papers + ]
Games are natural models for multi-agent machine learning settings, such as generative adversarial networks (GANs). The desirable outcomes from algorithmic interactions in these games are encoded as game theoretic equilibrium concepts, e.g. Nash and coarse correlated equilibria. As directly computing an equilibrium is typically impractical, one often aims to design learning algorithms that iteratively converge to equilibria. A growing body of negative results casts doubt on this goal, from non-convergence to chaotic and even arbitrary behaviour. In this paper we add a strong negative result to this list: learning in games is Turing complete. Specifically, we prove Turing completeness of the replicator dynamic on matrix games, one of the simplest possible settings. Our results imply the undecicability of reachability problems for learning algorithms in games, a special case of which is determining equilibrium convergence.
Sofic shifts are symbolic dynamical systems defined by the set of bi-infinite sequences on an edge-labeled directed graph, called a presentation. We study the computational complexity of an array of natural decision problems about presentations of sofic shifts, such as whether a given graph presents a shift of finite type, or an irreducible shift; whether one graph presents a subshift of another; and whether a given presentation is minimal, or has a synchronizing word. Leveraging connections to automata theory, we first observe that these problems are all decidable in polynomial time when the given presentation is irreducible (strongly connected), via algorithms both known and novel to this work. For the general (reducible) case, however, we show they are all PSPACE-complete. All but one of these problems (subshift) remain polynomial-time solvable when restricting to synchronizing deterministic presentations. We also study the size of synchronizing words and synchronizing deterministic presentations.
A growing number of machine learning architectures, such as Generative Adversarial Networks, rely on the design of games which implement a desired functionality via a Nash equilibrium. In practice these games have an implicit complexity (e.g. from underlying datasets and the deep networks used) that makes directly computing a Nash equilibrium impractical or impossible. For this reason, numerous learning algorithms have been developed with the goal of iteratively converging to a Nash equilibrium. Unfortunately, the dynamics generated by the learning process can be very intricate and instances of training failure hard to interpret. In this paper we show that, in a strong sense, this dynamic complexity is inherent to games. Specifically, we prove that replicator dynamics, the continuous-time analogue of Multiplicative Weights Update, even when applied in a very restricted class of games -- known as finite matrix games -- is rich enough to be able to approximate arbitrary dynamical systems. Our results are positive in the sense that they show the nearly boundless dynamic modelling capabilities of current machine learning practices, but also negative in implying that these capabilities may come at the cost of interpretability. As a concrete example, we show how replicator dynamics can effectively reproduce the well-known strange attractor of Lonrenz dynamics (the "butterfly effect") while achieving no regret.
We consider several computational problems related to conjugacy between subshifts of finite type, restricted to k-block codes: verifying a proposed k-block conjugacy, deciding if two shifts admit a k-block conjugacy, and reducing the representation size of a shift via a k-block conjugacy. We give a polynomial-time algorithm for verification, and show GI- and NP-hardness for deciding conjugacy and reducing representation size, respectively. Our approach focuses on 1-block conjugacies between vertex shifts, from which we generalize to k-block conjugacies and to edge shifts. We conclude with several open problems.
We extend and demonstrate the applicability of computational Conley index techniques for computing symbolic dynamics and corresponding lower bounds on topological entropy for discrete-time systems governed by maps. In particular, we describe an algorithm that uses Conley index information to construct sofic shifts that are topologically semi-conjugate to the system under study. As illustration, we present results for the two-dimensional Hénon map, the three-dimensional LPA map, and the infinite-dimensional Kot-Schaffer map. This approach significantly builds on methods first presented in [DFT08] and is related to work in [Kwa00, Kwa04].
A state amalgamation of a directed graph is a node contraction which is only permitted under certain configurations of incident edges. In symbolic dynamics, state amalgamation and its inverse operation, state splitting, play a fundamental role in the the theory of subshifts of finite type (SFT): any conjugacy between SFTs, given as vertex shifts, can be expressed as a sequence of symbol splittings followed by a sequence of symbol amalgamations. It is not known whether determining conjugacy between SFTs is decidable.
We focus on conjugacy via amalgamations alone, and consider the simpler problem of deciding whether one can perform k consecutive amalgamations from a given graph. This problem also arises when using symbolic dynamics to study continuous maps, where one seeks to coarsen a Markov partition in order to simplify it. We show that this state amalgamation problem is NP-complete by reduction from the hitting set problem, thus giving further evidence that classifying SFTs up to conjugacy may be undecidable.
Combining two existing rigorous computational methods, for verifying hyperbolicity [Arai, 2007] and for computing topological entropy bounds [Day et al., 2008], we prove lower bounds on topological entropy for 43 hyperbolic plateaus of the Hénon map. We also examine the 16 area-preserving plateaus studied by Arai and compare our results with related work. Along the way, we augment the entropy algorithms of Day et al. with routines to optimize the algorithmic parameters and simplify the resulting semi-conjugate subshift.
We present new methods of automating the construction of index pairs, essential ingredients of discrete Conley index theory. These new algorithms are further steps in the direction of automating computer-assisted proofs of semi-conjugacies from a map on a manifold to a subshift of finite type. We apply these new algorithms to the standard map at different values of the perturbative parameter ε and obtain rigorous lower bounds for its topological entropy for ε in [.7, 2].
The aim of this paper is to introduce a method for computing rigorous lower bounds for topological entropy. The topological entropy of a dynamical system measures the number of trajectories that separate in finite time and quantifies the complexity of the system. Our method relies on extending existing computational Conley index techniques for constructing semiconjugate symbolic dynamical systems. Besides offering a description of the dynamics, the constructed symbol system allows for the computation of a lower bound for the topological entropy of the original system. Our overall goal is to construct symbolic dynamics that yield a high lower bound for entropy. The method described in this paper is algorithmic and, although it is computational, yields mathematically rigorous results. For illustration, we apply the method to the Hénon map, wherne we compute a rigorous lower bound of 0.4320 for topological entropy.
In this paper, we classify and describe a method for constructing fractal trees in three dimensions. We explore certain aspects of these trees, such as space-filling and self-contact.