Lecture 30: Solving Recurrences
We looked at deriving recurrences for counting last lecture. We also started looking into solving the very simplest of recurrences. This lecture, we will look at some more interesting ways to tackle recurrences. Especially, we will introduce generating functions as an interesting way of solving recurrences.
Some Basic Summation Facts
We recall the following basic summation facts:
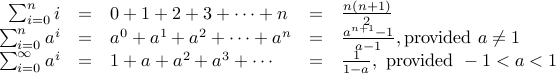
Given a knowledge of the closed forms of the summations above, we can calculate other kinds of summations. Let us take an example.
Example-1
Find the value of 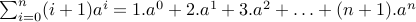 for some constant
for some constant  , where
, where 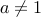 .
.
Let 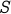 represent the value of the summation above.
represent the value of the summation above.
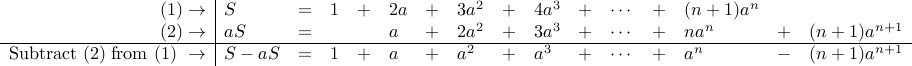
From the reasoning above, we get
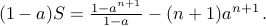
Since  , we conclude
, we conclude
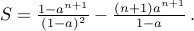
Solving Recurrences: Basics
We consider recurrences of the form: 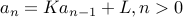 with base case
with base case 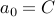 fixed.
fixed.
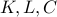 are constants.
are constants.
Example-1
Take the recurrence: 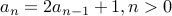 and
and 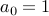 . Here is the derivation for the closed form.
. Here is the derivation for the closed form.
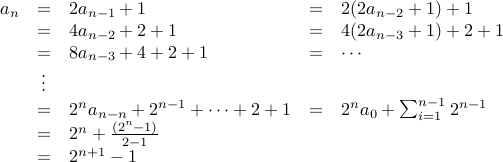
Observation
From the example above, we can proceed to solve recurrences of the form
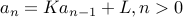 as follows:
as follows:
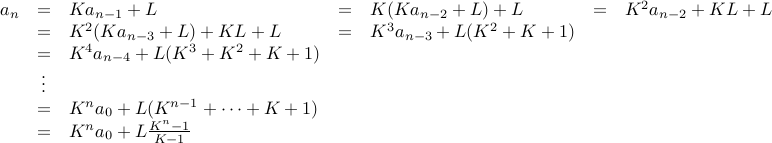
Second-Order Recurrences
We will now consider recurrences that are second-order of the form:
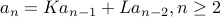
with base cases 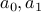 .
.
Well-Known examples of such recurrences include:
Fibonacci numbers:
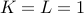 and
and 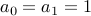 .
. Lucas Numbers:
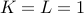 and
and 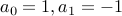 .
. Neganacci numbers:
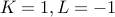 and
and 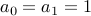 .
.
Quadratic Equation
For the second order recurrence
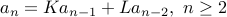
We setup a quadratic equation
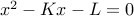
Let 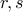 be two different roots to the quadratic equation above. Then the closed form solution to the recurrence
has the form
be two different roots to the quadratic equation above. Then the closed form solution to the recurrence
has the form
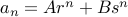
for some coefficients 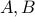 .
.
If the equation has a single repeated root 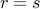 , then the solution is given by
, then the solution is given by
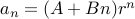
Example # 1
Consider the recurrence:
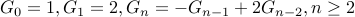
We write out some terms of this recurrence
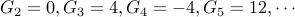 .
.
Here we have 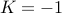 and
and 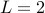 . Therefore we solve the quadratic equation:
. Therefore we solve the quadratic equation:
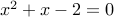
Its roots are: 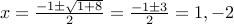 .
.
Therefore, the solution is of the form
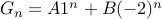
Given 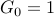 , we obtain
, we obtain 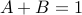 , and
, and 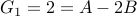 .
Solving, we obtain the solution
.
Solving, we obtain the solution
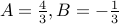
Therefore,
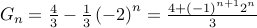 .
.
Example # 2
Consider the Fibonacci recurrence
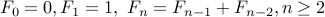 .
.
Here 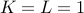 . The characteristic polynomial is
. The characteristic polynomial is
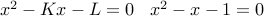 .
.
Solving this equation, we obtain the roots
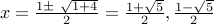 .
.
Therefore, the closed form is
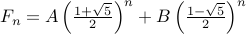 .
.
Plugging, in 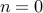 , we obtain,
, we obtain,
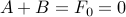 .
.
For 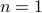 ,
,
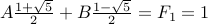 .
.
Writing 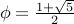 and
and 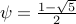 ,
we obtain the equations:
,
we obtain the equations:
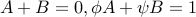
Solving them we obtain, 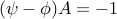 or
or 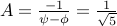 .
Likewise,
.
Likewise, 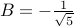 . The overall closed form is
. The overall closed form is
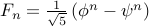 .
.
A special note: usually, we have Fibonacci numbers starting as 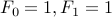 . The
closed form for the sequence with this base case will be
. The
closed form for the sequence with this base case will be
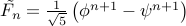 .
.