CSCI 2824: Lecture 15
This lecture will continue on
Partitions of a set: Definition.
Proving equivalences of sets (a couple of examples).
Material from book: 3.3.
Subsets
Given two sets  , and
, and 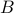 , we say that
, we say that 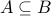 if every element of
if every element of  is an element of
is an element of 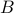 .
.
 is said to be a proper subset of
is said to be a proper subset of 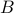 (written
(written 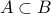 ) iff
) iff 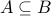 but at the same time
but at the same time 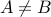 .
.
Two sets are equal, i.e, 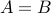 if and only if
if and only if 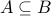 and
and 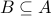 .
.
Power Sets
The power set of a set 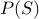 is the set that contains all subsets of
is the set that contains all subsets of 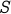 , including the empty set.
, including the empty set.
Let us first see some examples of power sets:
1. 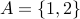 , its power set is
, its power set is 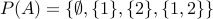 .
.
2. Take the empty set. Its power set is 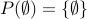 the set containing the empty set.
the set containing the empty set.
What is the difference between the empty set and set containing it? It is easy to explain through code.
Here is code to create empty set in C++ (you can write equivalent in Java):
set<int> * s = new set<int>(); // Create an empty set. assert( s-> size() == 0); // s has no elements
Here is how we create a set containing the empty set.
set<int> * emptySet = new set<int>(); // Create empty set. set< set<int>* > * emptyEmptySet = new set< set<int> > (); emptyEmptySet -> insert (emptySet); // Put the empty set into the empty empty. assert( emptyEmptySet -> size() == 1); // The size of the set containing the empty set is 1.
As you can see from the illustration above, the sets 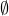 and its power set
and its power set 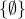 are indeed two different beasts!! The empty
set has cardinality zero whereas the power set of empty has cardinality
are indeed two different beasts!! The empty
set has cardinality zero whereas the power set of empty has cardinality 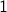 .
.
Counting the Elements of the Power Set
If set 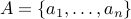 has
has 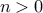 elements, how many elements does its power-set have?
elements, how many elements does its power-set have?
Let us take a smaller example 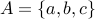 . And look at its power set. Each element of the power set is a
subset of
. And look at its power set. Each element of the power set is a
subset of  . We can visualize the power-set using the following table where a
. We can visualize the power-set using the following table where a  entry corresponding to
entry corresponding to 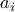 column
means that
column
means that 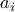 has been omitted from the subset.
has been omitted from the subset.
| Power set elt. | a? | b? | c ? |
| {} | 0 | 0 | 0 |
| {a} | 1 | 0 | 0 |
| {b} | 0 | 1 | 0 |
| {c} | 0 | 0 | 1 |
| {a,b} | 1 | 1 | 0 |
| {a,c} | 1 | 0 | 1 |
| {b,c} | 0 | 1 | 1 |
| {a,b,c} | 1 | 1 | 1 |
Note: We have established a one-one correspondence between the power set of  and a binary number of
and a binary number of 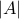 bits. In the example above,
bits. In the example above,
Every element of the power set of
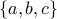 corresponds to a unique
corresponds to a unique 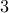 bit binary number.
bit binary number. Every
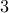 bit binary to an element of the power-set.
bit binary to an element of the power-set.
What about 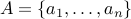 with
with  elements? Every element will correspond to a
elements? Every element will correspond to a  bit binary number. How many
bit binary number. How many  bit binary numbers
are there?
bit binary numbers
are there?
We have derived sufficient evidence to write the following theorem:
Theorem: The power set of  has
has 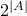 elements.
elements.
We can prove this claim in various ways. The one-one correspondence between elements of the power set and binary strings of
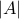 bits is the easiest proof. To convince ourselves fully that such correspondences can be used to count elements
in a set, we need to explore them further.
bits is the easiest proof. To convince ourselves fully that such correspondences can be used to count elements
in a set, we need to explore them further.
This naturally brings us to the topic of functions and one-to-one correspondences. Before that, we take a small diversion to define a partition here. It will be useful later when we study equivalence classes.
Partition
A parition, formalizes the idea of dividing up the elements of a set into  disjoint sets. Eg., Take a set
disjoint sets. Eg., Take a set 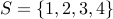 . An example
of a partition of
. An example
of a partition of 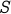 is
is 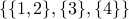 . Another example is
. Another example is 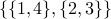 .
.
A partition of a set 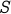 is a set of subsets
is a set of subsets 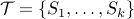 such that
such that
None of the
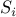 s are empty:
s are empty: 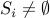 for
for 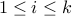 .
. Every pair of elements
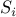 and
and 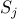 are disjoint:
are disjoint: 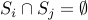 for
for 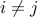 .
. The union of all elements gives
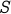 :
: 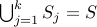 .
.
True or False: Any partition 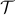 of a set
of a set 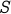 is a subset of its power set
is a subset of its power set 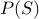 .
.
Factoid
Here is a problem about partitions: You are given a set of numbers 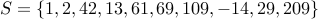 . The question is
whether we can partition
. The question is
whether we can partition 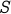 into two subsets
into two subsets
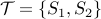 such that the sum of elements in
such that the sum of elements in 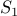 is the same as the sum in
is the same as the sum in 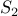 .
.
This problem has applications all over the place but is known to be a hard problem (as hard as factoring integers).
Proving Properties of Sets
We are often asked to prove certain relations between two sets: they are the same or that one is a subset of another. These proofs tend to be simple provided our approach to them is systematic. Here are a couple of examples:
Example-1
Claim For any three sets 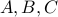 , we have
, we have 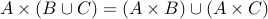 .
.
To prove that two sets are the same, we show that each one is the subset of the other.
Prove
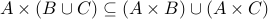 .
. Take any element
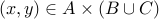 . We will show that
. We will show that 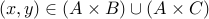 .
. We know that by definition,
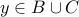 . In other words,
. In other words, 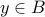 or
or 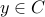 .
. If
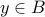 ,
, 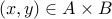 .
. Otherwise, if
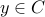 , we have
, we have 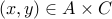 .
.
Therefore, we conclude that
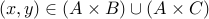 .
.
Prove
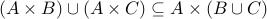 .
. Once again, let us take any element
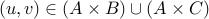 . We will show that
. We will show that 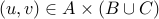 .
. We know that either
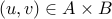 or
or 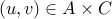 .
. Therefore, we conclude that
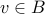 or
or 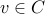 .
. I.e,
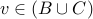 .
. Putting this together, we get
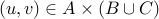 .
.
Example-2
Claim Given two sets 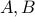 ,
, 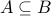 holds if and only if
holds if and only if 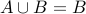 .
.
Notice that the claim is an if and only if claim. Such claims are actually two subclaims in disguise. We need to prove each of them.
Subclaim-1: For any sets
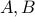 , IF
, IF 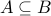 then
then 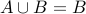 .
. Subclaim-2: For any two sets
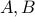 , IF
, IF 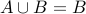 then
then 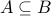 .
.
Let 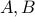 be any two given sets such that
be any two given sets such that 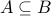 holds. We will show that
holds. We will show that 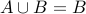 holds.
holds.
To show 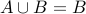 , we will first show that (1.)
, we will first show that (1.) 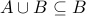 and (2.)
and (2.) 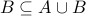 .
.
Proof of
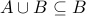 : Take any element of
: Take any element of 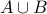 and show that it also belongs to
and show that it also belongs to 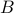 .
.Let
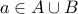 . We know that
. We know that 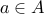 or
or 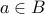 . However, since
. However, since 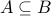 , we know that
, we know that 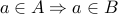 . Therefore, we can safely conclude that
. Therefore, we can safely conclude that 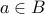 . Therefore
. Therefore 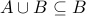 .
.
Proof of
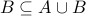 : Take any element of
: Take any element of 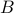 and show that it also belongs to
and show that it also belongs to 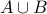 .
.Let
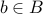 . By definition of union, we conclude that
. By definition of union, we conclude that 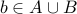 .
.
For any two sets 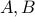 , IF
, IF 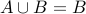 then
then 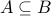 .
We will attempt a proof by contradiction.
.
We will attempt a proof by contradiction.
Let
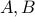 be any two sets such that
be any two sets such that 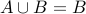 . However for the sake of contadition, we assume that
. However for the sake of contadition, we assume that 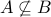 . Therefore, there is some element
. Therefore, there is some element 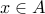 such that
such that 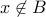 .
. However, since
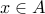 , we have that
, we have that 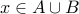 . However,
. However, 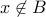 . Therefore,
we have proved that
. Therefore,
we have proved that 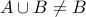 since one of the sets has
since one of the sets has 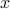 in it and the other does not.
in it and the other does not.
This however, contradicts our assumption that 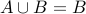 .
.