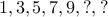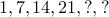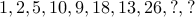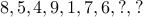CSCI 2824: Lecture #2 Notes
In this lecture we will cover the basic notation for sequences and summation.
Concepts learned:
Representing sequences: closed form, recurrence relation. Ordinal notation for sequences.
Converting recurrences to closed forms (very basics).
Summations and summation notation.
Extra: Alphabet sequences.
Sequences
We have seen this puzzle. Some one gives you a sequence of numbers and asks you to guess the next number. Often it is easy enough to do that. Sometimes, it can get really tricky!
Guess the next number(s) in the following sequence:
A common trick (a lot of IQ tests use) is to mix two simple ones into a seemingly complex one:
How about this one?
Working hard on a sequence, try this cool site: Online Encylopedia of Integer Sequences! :-)
How do we talk about sequences mathematically?
We use the notation 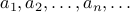 to denote a sequence.
to denote a sequence. 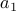 is the
is the 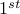 element. Likewise, the
element. Likewise, the
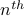 element is written
element is written 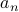 (pronounced ’’ a sub n’’).
(pronounced ’’ a sub n’’).
A sequence can be specified in two ways:
Closed-Form Representation: We write
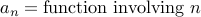 that holds for all
that holds for all 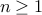 .
. Recurrence Relation: This is also called a Recursive Formula or simply a recurrence. A sequence can be written as a recurrence by writing
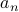 in terms of
in terms of 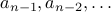 and specify a base case for
and specify a base case for 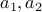 and so on.
and so on.
We will now give examples to illustrate both ways in detail starting with the recurrence for a sequence.
Recursive Formulae
Each recursive formula or recurrence has two parts to it.
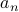 written as a function of
written as a function of 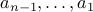 .
. A starting value or a base case for
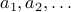 .
.
This will be clear once we work through some examples. Let us start with some examples of recurrences.
Example-1 (Even Numbers)
We have the following recurrence for even numbers:
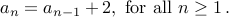
with the base case:
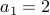
Do not forget the base case and note that recurrence holds only for n >= 1
We can think of a recurrence as a simple recursive program. Here is how the recurrence above translates into C/C code:
/* Recursive formula is implemented by a recursive function */ int A( int n) { assert(n >= 0); if ( n == 1) return 2; return A(n-1) + 2; }
Question: What happens to the code above, if we forgot the base case?
We saw an example where 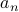 was related just to
was related just to 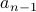 . However, recurrences can be more general.
. However, recurrences can be more general.
Example 2: Fibonacci Numbers
Fibonacci Numbers were invented by the famous Italian mathematician Leonardo Fibonacci. Interestingly these numbers turn up all over the place, often for reasons that are not well understood. They are closely related to the golden ratio. For more Fibonacci-ology see the Wikipedia Article.
Fibonacci numbers can be written as the recurrence:
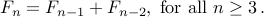
We have to give two base cases:
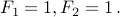
Question to class: Why do we need to specify 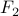 ?
?
Notice that since we have to give base cases for 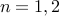 , the recurrence is applied for
, the recurrence is applied for 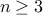 .
.
If you think in code (like me), then consider this very simple piece of code to compute the Fibonacci numbers:
/* CS majors: Coding up Fibonacci numbers is a common job interview (trap) question */ /* If you are ever challenged to do so, do not write this code below. */ int F ( int n){ assert ( n >= 1); if (n == 1) return 1; if (n == 2) return 1; return F(n-1) + F(n-2); }
Delete the ’'if’’ statement that handles the base case for 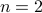 and see what happens.
and see what happens.
Coding Question: The code above is a really really inefficient way to compute Fibonacci numbers. Can you say why?
Hint Try computing 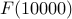 and go take a long walk in the woods :-)
and go take a long walk in the woods :-)
A More Complex Recurrence
Let us try a more complex recurrence (more complex than the ones we have seen so far, at least):
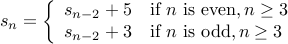
Base Cases for the Recurrence
What bases cases should be specified for this recurrence?
To answer this, let us ’'run’’ this recurrence for some values of 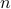 .
.
Compute 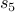 : Since
: Since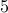 is odd, we use the recurrence for odd numbers:
is odd, we use the recurrence for odd numbers:
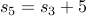
Now let us expand 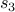 further:
further:
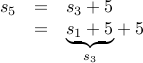
We have no rule for expanding 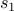 , so we have to specify it as a base case.
, so we have to specify it as a base case.
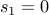
Compute  : Following the definition,
: Following the definition,
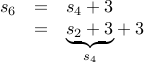
Again, we have no rule for expanding 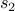 . So we have to specify it as a base case:
. So we have to specify it as a base case:
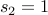
Putting it together
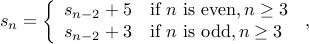
with the base cases given by 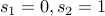 .
.
We obtain the sequence:
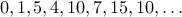
Looks complicated, but it is actually two sequences ’'zipped’’ together.
Collatz Recurrence
This is one more famous (and crazy!!) recurrence defined as follows:
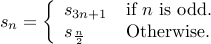
Base case is: 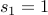 .
.
Claim: 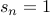 for all
for all 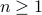 .
.
No one has been able to prove it. To see why let us try an example:
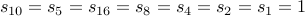
Let us try one more:
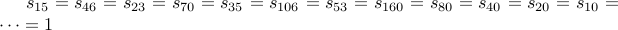
Here is the code for printing out the the sequence of indices encountered through the recurrence above:
#include <stdio.h> int C (int n) { assert ( n >= 1); printf ("Collatzing through %d \n", n); if (n == 1) return 1; /* n is even? */ if (n %2 == 0) return C(n/2); /* n is odd */ return C( 3 * n + 1); }
The claim above can be interpreted as saying that Collatz's recurrence code above always halts and outputs
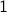 for any integer
for any integer 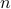 . Can you try proving that the code above terminates?
. Can you try proving that the code above terminates?
Exercise: Try running the code above for 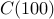 ,
, 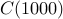 and so on. You will see the sequence go up to
really large numbers before coming back down to
and so on. You will see the sequence go up to
really large numbers before coming back down to 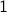 , magically. At some point, however, an integer overflow
on your machine could happen and the result could be meaningless.
, magically. At some point, however, an integer overflow
on your machine could happen and the result could be meaningless.
Random Number Generator
Here is an interesting fact: sequences defined using recurrence relations are used inside computers to generate pseudo random numbers. The most common sequence used is a Linear Congruential Generator.
Ill Defined (Nonsensical) Recurrences
Note that we have carefully avoided the topic of “well-definedness” of a recurrence. We provide a quick introduction here.
It turns out that not all recurrences or recursive formulae are well defined. A formula defining 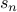 recursively
is well defined if for every
recursively
is well defined if for every 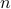 it can be used to compute
it can be used to compute 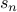 uniquely.
uniquely.
Some of them are plain ’'nonsense’’.
Here are some examples. Can you spot the problems?
1. 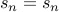 , with base case
, with base case 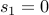 . This does not define a unique sequence. Every sequence beginning with a
. This does not define a unique sequence. Every sequence beginning with a  can fit this definition. If you implemented this in code, it will just loop forever.
can fit this definition. If you implemented this in code, it will just loop forever.
2. 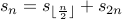 , with
, with 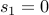 . Once again, if you implemented this in code, it will go into an infinite loop or number overflow.
. Once again, if you implemented this in code, it will go into an infinite loop or number overflow.
As a good rule of thumb: a recurrence is ill defined if writing it out as a program in CCJava or whatever, causes the code
to go into an infinite loop for some number 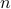 .
.
Diversionary Note: Finding out if a recurrence is well-defined is a really hard problem (it is equivalent to the halting problem for computers).
Closed Form Representation
Another way of representing sequences is through the closed form. In the closed form
representation, we simply express 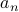 as an expression over
as an expression over 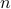 for all
for all 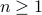 .
.
Here is the closed form representation for the sequence of even numbers:
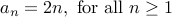
Simple, no fuss.
However, closed form representations are not that easy to get always. Let us try some examples.
Squares
Consider the recurrence for 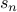 given by
given by
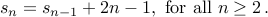
with base case
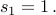
Let us try computing some values.
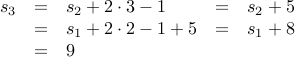
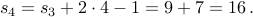
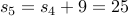
The closed form for this recurrence is
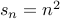
In a couple of weeks, we will look at induction proofs of this fact
Fibonacci Numbers
Closed forms are not always ’'simpler’’ than the original recurrences.
Recall the recurrence for Fibonacci numbers:
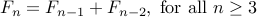
with base case 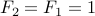 .
.
The closed form for the  Fibonacci number is given by the
Binet formula:
Fibonacci number is given by the
Binet formula:
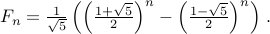
You will be asked to prove this fact. In fact, you will find that it is not all that hard once we really get going in this course!!
Here is the cool fact. The number
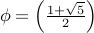
has a special name. It is called the Golden Ratio. Among other things, the rectangle whose sides are in the golden ratio seems to be the most ’'aesthetically pleasing’’ to the human eye!!
Using this fact, we can write Fibonacci numbers as:
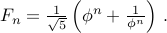
Diversionary Note: We can use this formula to write a computer program that is truly efficient for
computing  . Such a program can compute a
. Such a program can compute a  for
for 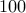 digit
digit
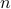 in roughly
in roughly 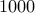 or so arithmetic operations (if you assume that
overflows do not happen). Can you attempt to write it? As a hint, you do not need to know
the value of
or so arithmetic operations (if you assume that
overflows do not happen). Can you attempt to write it? As a hint, you do not need to know
the value of 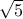 , to code this up.
, to code this up.
Sequences that Cannot be Represented Easily
It needs to be mentioned that there are many sequences that are not easily represented either as a closed form or as a recurrence.
The sequence of prime numbers is one such sequence.
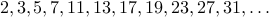
We do not have a ’'easy’’ closed form for the 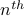 prime number (there are some
really complicated ones that are not worth going into). Same holds for
recurrences: the known ones are quite complicated.
prime number (there are some
really complicated ones that are not worth going into). Same holds for
recurrences: the known ones are quite complicated.
Summation
Given a sequence of numbers 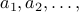 (defined using closed form or a recurrence), we define the summation of the
first
(defined using closed form or a recurrence), we define the summation of the
first 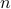 terms of the sequence as
terms of the sequence as
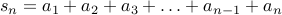
We write this summation succinctly as:
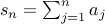
The symbol  is the summation operator. The notation
is the summation operator. The notation 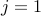 at the bottom of the summation is
the lower limit of the sum and the
at the bottom of the summation is
the lower limit of the sum and the 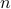 at the top is the upper limit.
at the top is the upper limit.
Once again we think in terms of code:
int SumSequence(int n, int [] A){ int j; int sum = 0; for (j=1; j <= n; ++j){ sum = sum + A[j]; } return sum; }
If the sequence 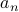 is given, then the summation of its first
is given, then the summation of its first 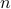 terms
terms 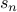 itself
is a sequence given by the following recurrence:
itself
is a sequence given by the following recurrence:
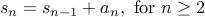
with the base case

Take the sequence 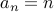 written in the closed form for convenience. What about the
summation of the first
written in the closed form for convenience. What about the
summation of the first 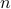 terms of this sequence?
terms of this sequence?
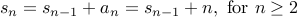
The base case is 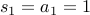 .
.
The closed form for 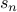 (the summation) is given by
(the summation) is given by
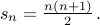
It is really the summation of first 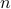 numbers. Here is how the
numbers. Here is how the 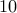 year old Gauss supposedly (and famously) reasoned this out:
year old Gauss supposedly (and famously) reasoned this out:
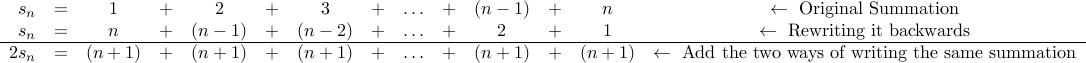
The last equation gives us
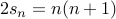
which gives us the required closed form for 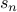 .
.
Observation Getting closed form representations for sequences and summations is often a difficult art in itself. Carl Fredrich Gauss was one of the unrivalled master at this!!
Beyond Number Sequences
We just noticed how sequences of numbers can be represented either by a closed form or by a recurrence. In computer science, we often represent other sequences using such recursive formulae or recurrences. We will keep seeing examples of these throughout this course. The generalization of sequences are called ’'inductive definitions’’ and sometimes they are called ’'grammars’’. Here is a quick primer on grammars. CSCI 3434 (Mathematical Theory of Computation )and the compilers course cover a lot more on this.
Sequences of Letters
Let us assume that there are two letters 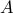 and
and 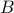 . We can define sequences of ’'words’’ over these letters:
. We can define sequences of ’'words’’ over these letters:
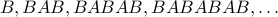
The recurrence for such sequences is often called a ’'grammar’’ and written slightly differently (after the work of computer scientists and linguists such as Chomsky, Naur, …).
The recurrence is given by
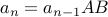
which means, that the 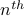 element of the sequence is the
element of the sequence is the 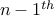 element with
the characters AB tacked on to the end. The base case is given by
element with
the characters AB tacked on to the end. The base case is given by
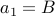
Here is a more complex (context-free) recurrence relation:
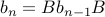
with 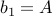 as the base case.
as the base case.
What is the sequence obtained here?
Answer: 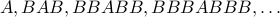 .
.
Interestingly, the theory behind formal grammars is the basis for how we write compilers for programming languages. It is one of the most important applications of theoretical computer science or discrete mathematics to computer science.
Simultaneous Recurrences
Not covered in class. For your own interest.
Simultaneous recurrences involve two or more sequences that mutually depend on each other. Perhaps, an example is the best way of explaining.
We define two sequences 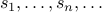 and simultaneously
and simultaneously 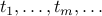 in terms of each other.
Here is an example:
in terms of each other.
Here is an example:
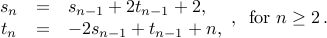
with base case:
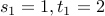
The code for such a recurrence involves mutual recursive functions.
extern int S( int n); /* Declare S,T in advance */ extern int T( int n); int S( int n) { assert( n >= 1); if (n==1) return 1; return S(n-1) + 2 * T(n-1) + 2; } int T(int n) { assert( n >= 1); if (n==1) return 2; return T(n-1) -2 * S(n-1) + n; }
The study of these recurrences is beyond the scope of this class. Yet, they produce some very interesting phenomena called chaotic dynamics. It turns out that some of these recurrences (eg., see the Henon map) can have very complex behaviours as the base case for the recurrence is modified. For more, you will have to take the course CSCI 4446 on Chaotic Dynamics or equivalent applied maths/physics class.