RSA Algorithm
We talked about the ideas behind public key cryptography last lecture. How do we implement such a scheme? This is where number theory comes to the rescue in the form of the RSA crypto system. RSA stands for Rivest, Shamir and Adelman, who discovered the scheme in 1977. Clifford Cocks had independently discovered this earlier in 1973, but his work was classified and remained unknown for many years.
A link to the original RSA paper is here.
Messages As Numbers
First, let us get some preliminary concepts out of the way. We will regard messages as numbers. The idea is that your message is encoded as a number through a scheme such as ASCII. The rest of this presentation will deal with encrypting and decrypting numbers.
Basic Idea
Suppose Alice wished to send a message 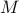 to Bob that she wished Bob
and no one else to read. In a public key system, she will obtain Bob's
public key and encrypt the message
to Bob that she wished Bob
and no one else to read. In a public key system, she will obtain Bob's
public key and encrypt the message 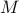 using Bob's public key to
obtain a encrypted message
using Bob's public key to
obtain a encrypted message  . This is sent to Bob.
. This is sent to Bob.
Upon receiving the message from Alice, Bob decrypts it using his private key. No one else can decrypt the message unless they have Bob's private key.
How do we implement this in practice?
The basic idea behind RSA is to create a one-way function 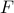 that
given a message
that
given a message 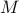 and a public key
and a public key 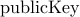 , encrypts the
message by computing
, encrypts the
message by computing 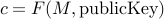 to yield the cipher
to yield the cipher
 .
.
The reason 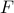 is called one-way is that
is called one-way is that
Given
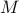 and
and 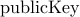 , it is easy to compute
, it is easy to compute 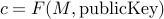 to encrypt
to encrypt 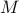 .
.However, someone who is snooping the channel sees
 and
and 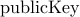 . It is computationally hard to invert
. It is computationally hard to invert 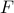 and compute the original message
and compute the original message 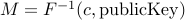 .
.
However, if it is hard for someone to invert 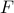 , how is it that Bob can do so?
, how is it that Bob can do so?
We will assume that using the private key, Bob has a function
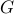 that
will allow him to compute
that
will allow him to compute 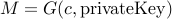 .
.
So our scheme should give us functions 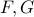 where
where 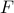 is easy to
compute but very hard to invert. On the other hand,
is easy to
compute but very hard to invert. On the other hand, 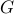 is easy to
compute and inverts
is easy to
compute and inverts 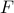 if the private key is available.
if the private key is available.
Number Theory to the Rescue
The basic scheme for RSA uses a really large number  .
.
The public key is a pair of numbers
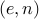
The private key is a pair of numbers
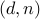 .
.
Each message 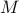 is assumed to be a number between
is assumed to be a number between 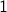 and
and 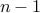 . If
. If
 is really large, we allow a large space of numbers to code our
messages with.
is really large, we allow a large space of numbers to code our
messages with.
The basic idea is to encrypt a message 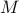 by computing
by computing 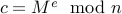 . This operation is called modular exponentiation. It is
computationally inexpensive to compute even though
. This operation is called modular exponentiation. It is
computationally inexpensive to compute even though 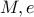 and
and  are
typically large numbers in an RSA implementation.
are
typically large numbers in an RSA implementation.
Let us take a message 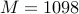 and encrypt it using the public key
and encrypt it using the public key
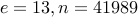 .
.
We will simply compute
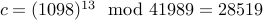
On the first sight, this modular exponentiation looks like an
atrociously hard computation. But remember that 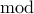 is
infectious :-).
is
infectious :-).
Therefore, we can first compute this by repeated squaring and modulo operations. Here is how we compute for our example using python interpreter
bash$ python Python 2.7.6 (v2.7.6:3a1db0d2747e, Nov 10 2013, 00:42:54) [GCC 4.2.1 (Apple Inc. build 5666) (dot 3)] on darwin Type "help", "copyright", "credits" or "license" for more information. >>> c1 = (1098 **2) % 41989 >>> c1 29912 >>> c2 = (c1 **2) % 41989 >>> c2 26132 >>> c3 = (c2 **2) %41989 >>> c3 14317 >>> c4 = (c3 * c2) % 41989 >>> c4 9854 >>> c5 = (c4 * 1098) % 41989 >>> c5 28519
However, a snooper who simply sees the encrypted message  and the
public key
and the
public key 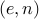 will find it very hard to figure out the message
will find it very hard to figure out the message
 . This problem is considered to be a computationally hard problem,
and is called the RSA problem.
. This problem is considered to be a computationally hard problem,
and is called the RSA problem.
So far, we have identified our one way function 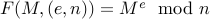 ,
which is given by modular exponentiation . We have claimed that inverting
,
which is given by modular exponentiation . We have claimed that inverting
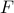 when given
when given  and the public key
and the public key 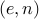 is computationally a hard problem.
There is no known efficient algorithm for this problem, to date.
is computationally a hard problem.
There is no known efficient algorithm for this problem, to date.
Now the idea is to find a private key 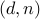 that satisfies
that satisfies 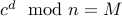 . In other words, if we take the encrypted message
. In other words, if we take the encrypted message  and
perform modular exponentiation with the private key
and
perform modular exponentiation with the private key 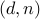 , we obtain
the original message
, we obtain
the original message 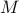 back.
back.
This means that we need 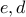 to satisfy the property that for any message
to satisfy the property that for any message
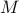 ,
,
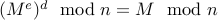
In other words, we require that
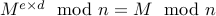 .
.
The question is how can we find a pair 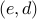 that will satisfy this
relation, and furthermore, given
that will satisfy this
relation, and furthermore, given 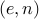 it should be hard to find the
corresponding
it should be hard to find the
corresponding 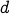 .
.
Some Preliminaries
We say that two numbers 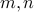 are relatively prime if they have no prime
factors in common. In other words,
are relatively prime if they have no prime
factors in common. In other words, 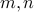 are relatively prime if their
greatest common divisor
are relatively prime if their
greatest common divisor 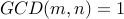 .
.
10 and 21 are relatively prime numbers. The prime factors of 10 are
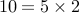 and
and 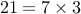 . Thus, they have no prime
factors in common.
. Thus, they have no prime
factors in common.
On the other hand 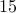 and
and 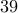 are not relatively prime. They have a prime
factor
are not relatively prime. They have a prime
factor 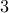 in common.
in common.
By convention, 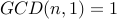 for all
for all  . Therefore,
. Therefore, 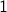 is taken to
be relatively prime to every other non-zero number.
is taken to
be relatively prime to every other non-zero number.
Euler's Theorem
You can skip this section on a first read
The answer comes from a result proved by Euler in 1741, called the Euler's Totient theorem. We will first examine the Totient function.
Given a number  , its totient
, its totient 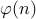 is the total number
of integers between
is the total number
of integers between 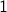 and
and 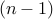 that are relatively prime
with
that are relatively prime
with  .
.
As an example, consider 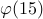 . The numbers
that are relatively prime to
. The numbers
that are relatively prime to 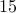 include
include
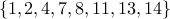 .
.
Therefore 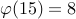 .
.
Interestingly, given a number  ,
, 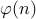 is rather hard to
compute. But there are numbers for which it is relatively easy.
is rather hard to
compute. But there are numbers for which it is relatively easy.
Theorem: The totient function 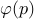 for a prime number
for a prime number 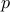 is simply
is simply 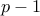 .
.
The proof is simply to note that every number 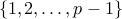 is
relatively prime to
is
relatively prime to 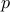 .
.
Another important result about Totient functions is as follows:
If 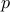 and
and 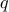 are prime numbers, such that
are prime numbers, such that 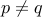 , then
, then
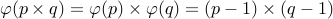 .
.
Let us look at all numbers between 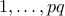 that have a common
factor with
that have a common
factor with 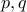 . These can only be multiples of
. These can only be multiples of 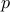 or multiples of
or multiples of
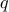 . The reader can convince themselves that there are
. The reader can convince themselves that there are 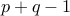 of
these numbers. Therefore,
of
these numbers. Therefore, 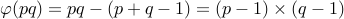 .
.
Here is what Euler's theorem says:
Let 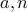 be relatively prime numbers. We have
be relatively prime numbers. We have 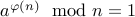 .
.
The proof is rather elegant. Let 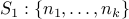 be the
set of all the numbers relatively prime with
be the
set of all the numbers relatively prime with  . Here
. Here 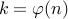 and
and  belongs to this set. Now consider
belongs to this set. Now consider 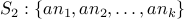 . It is possible to show that
. It is possible to show that 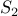 and
and 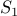 are, in fact, the same sets.
are, in fact, the same sets.
Therefore,
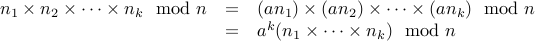
We therefore conclude that 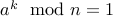 , or in other words
, or in other words
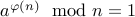 .
.
RSA Scheme
We are now ready to talk about the basic RSA scheme.
The idea is to choose two different large prime numbers 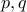 and
compute
and
compute 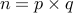 . Let us assume
. Let us assume 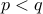 , in general.
, in general.
We now wish to find a pair 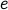 and
and 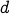 for the public and private keys such that
for any message
for the public and private keys such that
for any message 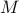 , we have
, we have 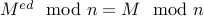 .
.
Choosing any message 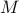 between
between 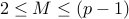 , we can use
Totient's theorem to guarantee that
, we can use
Totient's theorem to guarantee that
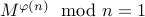 .
.
Therefore, if we choose any positive  , we still obtain
, we still obtain
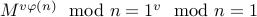 .
.
Therefore, 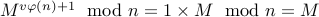 , for
any
, for
any 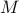 .
.
Our goal is now to find 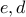 such that
such that
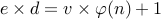 .
.
In other words, 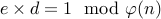 .
.
We follow the following steps to do so:
Choose large primes
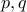 with
with 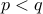 .
.Let
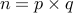 .
.Let
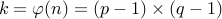 .
.Choose a number
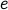 with
with 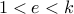 that is relatively prime with
that is relatively prime with  .
.Compute
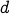 such that
such that 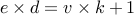 for some
for some  . This
is done using the Euclidean Algorithm.
. This
is done using the Euclidean Algorithm.
Finally, we discard 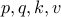 and simply retain
and simply retain 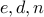 . We publish
. We publish 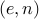 as the public key and retain
as the public key and retain 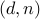 as the private key.
as the private key.
Encrypting a message 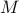 is performed by modular exponentiation with
public key:
is performed by modular exponentiation with
public key:
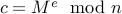 .
.
Likewise, decryption uses the private key 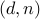 .
.
Given cipher-text  , we recover the original message as
, we recover the original message as
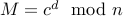
Let us illustrate this:
Choose
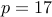 and
and 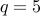 . We have
. We have 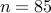 and
and 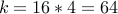 .
.Let us choose
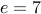 .
.We have to find
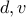 so that
so that 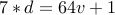 . We have
. We have 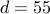 and
and  .
.Verify that
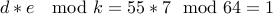 .
.The private key is
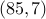 . The public key is
. The public key is 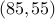 .
.
Encryption: Take a message 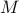 represented as a number from
represented as a number from 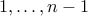 . The encrypted value of
. The encrypted value of 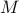 is
is  .
.
Example: Using public key 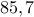 and message
and message 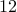 , we have
, we have 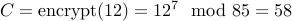 .
.
To decrypt, we have to compute  =
= 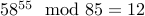 .
.
Breaking RSA
Let us assume that some one has access to the public key 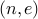 . What stops them from finding out
. What stops them from finding out 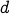 , the secret key?
, the secret key?
After all, 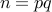 . Therefore, by factorizing
. Therefore, by factorizing  , we can find
, we can find 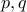 and repeat the process for ourselves to compute
and repeat the process for ourselves to compute 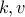 and
and 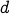 . Once
. Once 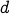 is known then the whole scheme goes kaput.
is known then the whole scheme goes kaput.
Problem (Factoring) Given a number  that we are told is the
product of two as yet unknown prime numbers
that we are told is the
product of two as yet unknown prime numbers 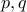 , finding out
, finding out 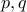 is a hard problem.
is a hard problem.
In order to convince you that factoring a large number say 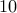 digits
is hard, your first programming assignment that will be out this
monday asks you to try and write a factoring routine that given a
number
digits
is hard, your first programming assignment that will be out this
monday asks you to try and write a factoring routine that given a
number  finds a prime factor
finds a prime factor 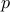 of
of  . You can use any method to
do so.
. You can use any method to
do so.
Combinatorially Hard Problems
There are problems in CS which do not have any known algorithms. The class of problems is called NP standing for Non-Deterministic Polynomial Time.
Claim Factoring a number  is an example of a hard problem.
is an example of a hard problem.
int factor(int n){ int i; for (i = 0; i < n;++i) if (Divides(i,n)) return i; return NO_FACTOR; }
Time taken to factor by best known algorithm is roughly  .
However, does that preclude a clever and faster algorithm?
.
However, does that preclude a clever and faster algorithm?
The best known factoring algorithm is the general number field sieve. Even though
it is worst case exponential, it has been used to factor large number of upto a 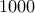 decimal
digits.
decimal
digits.