CSCI 2824 Lecture 19: Properties of Relations
We will now restrict ourselves to relations 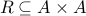 for a set
for a set  . Such relations can be viewed
as a graph.
. Such relations can be viewed
as a graph.
Graphs and Relations
Relations 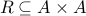 with domain and co-domain as the same
set
with domain and co-domain as the same
set  can be viewed as a graph.
can be viewed as a graph.
A graph  consists of a set
consists of a set  of nodes and a relation
of nodes and a relation 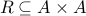 of edges. Each edge in a graph
of edges. Each edge in a graph 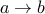 corresponds to a pair
corresponds to a pair 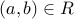 .
.
It is a common convention to call the set of nodes 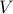 (rather than
(rather than
 ) edge relation
) edge relation 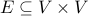 (rather than
(rather than  ) if we are talking about a graph. But we will ignore this
convention for now.
) if we are talking about a graph. But we will ignore this
convention for now.
We will look at two examples of relations and their corresponding graphs.
Example # 1
Consider the relation 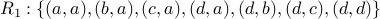 over the set of nodes
over the set of nodes 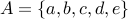 . Its graph is depicted
below:
. Its graph is depicted
below:
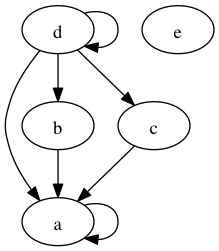
Note that the graph has a node 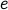 without any links. This is because
without any links. This is because
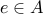 but there is no tuple involving
but there is no tuple involving 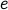 in the relation
in the relation 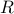 that
describes the edge set.
that
describes the edge set.
Next, note that the edges corresponding to 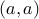 and
and 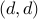 are
called self-loops. The graph of the relation in this example has two
self loops, one over
are
called self-loops. The graph of the relation in this example has two
self loops, one over  and the other over
and the other over 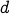 .
.
Example # 2
Consider the relation 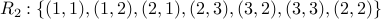 over the set of nodes
over the set of nodes 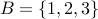 . Its graph is depicted
below:
. Its graph is depicted
below:
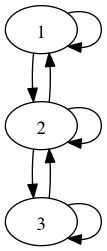
Note that the arrow from 1 to 2 corresponds to the tuple 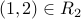 , whereas the reverse arrow from
, whereas the reverse arrow from 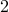 to
to 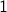 corresponds to the tuple
corresponds to the tuple 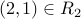 .
.
Types of Relations
We first study three types of relations: reflexive, symmetric and transitive.
A relation 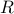 is reflexive iff
is reflexive iff 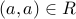 for all
for all 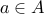 .
.
From the graph, we note that a relation is reflexive if all nodes in the graph have self-loops
The relation 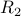 from example #2 above is reflexive whereas the
relation
from example #2 above is reflexive whereas the
relation 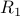 from example #1 is not.
from example #1 is not. 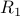 is missing the self loops
from
is missing the self loops
from 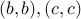 and
and 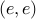 .
.
The next concept is that of a symmetric relation.
A relation 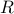 is symmetric iff for all
is symmetric iff for all 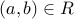 ,
, 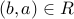 .
.
From its graph, a relation is symmetric if for every “forward” arrow from  to
to 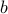 , there is also a reverse arrow from
, there is also a reverse arrow from 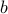 to
to  .
.
The relation 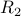 from example #2 above is symmetric whereas the
relation
from example #2 above is symmetric whereas the
relation 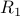 from example #1 is not.
from example #1 is not. 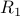 has the edge
has the edge 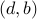 but
not the reverse edge
but
not the reverse edge 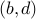 .
.
Finally, we will talk about transitive relations.
A relation 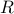 is transitive iff for all a,b,c, IF
is transitive iff for all a,b,c, IF 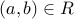 and
and 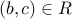 THEN
THEN 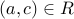 .
.
In graph terms, if we start at some node  , and using an edge go from
, and using an edge go from  to
to 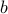 and then from
and then from 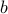 to
to  using another edge, we should also be able to go from
using another edge, we should also be able to go from  to
to  directly using an edge.
directly using an edge.
The relation 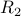 from example #2 above is not transitive. It is
missing the edges
from example #2 above is not transitive. It is
missing the edges 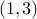 and
and 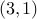 , that would make it transitive.
The relation
, that would make it transitive.
The relation 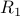 from example #1 is transitive, on the other hand.
from example #1 is transitive, on the other hand.
Putting all these together, a relation is an equivalence iff it is reflexive, symmetric and transitive.
We now consider the polar opposite of a reflexive relation, an irreflexive relation:
A relation 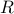 is irreflexive iff
is irreflexive iff 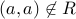 for all
for all 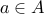 .
.
For all 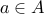 , we have
, we have 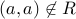 .
.
While a reflexive relation has all the self-loops, an irreflexive one has no self-loops.
The relation 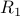 in example # 1 is not irreflexive since it has
self-loops
in example # 1 is not irreflexive since it has
self-loops 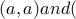 d,d)$. Removing these from the relations
yields us an irreflexive relation
d,d)$. Removing these from the relations
yields us an irreflexive relation
Example
Take the set 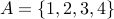 . Give us examples of relations that are
. Give us examples of relations that are
Reflexive:
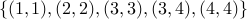 .
. Irreflexive:
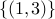 . Caution Irreflexive is not the logical negation of reflexive. It is stronger than that.
. Caution Irreflexive is not the logical negation of reflexive. It is stronger than that. Symmetric:
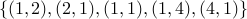 .
. Transitive: example in class.
Equivalence:
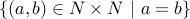 .
. Equivalence-2:
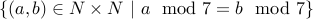 .
.
What about the empty set as a relation? Is it reflexive? Symmetric? Transitive??
Example
Conider the standard  relation over
relation over 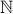 .
.
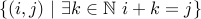
It is reflexive since
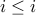 for all
for all 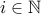 .
.It is not symmetric:
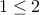 but
but 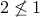 .
.It is transitive:
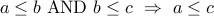 .
.It is not irreflive since
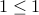
Anti-Symmetric Relation
We looked at irreflexive relations as the polar opposite of reflexive (and not just the logical negation). Now we consider a similar concept of anti-symmetric relations.
This is a special property that is not the negation of symmetric.
A relation 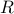 is anti-symmetric iff whenever
is anti-symmetric iff whenever 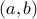 and
and 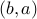 are both in
are both in 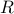 then
then 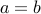 .
.
Anti-symmetric is not the opposite of symmetric. A relation can be both symmetric and anti-symmetric:
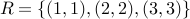
Another example is the empty set. It is both symmetric and anti-symmetric.
The  relation on
relation on 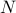 is anti-symmetric. Whenever
is anti-symmetric. Whenever 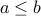 and
and 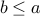 then
then 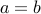 . In fact, the notion
of anti-symmetry is useful to talk about ordering relations such as
. In fact, the notion
of anti-symmetry is useful to talk about ordering relations such as 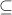 over sets and
over sets and  over natural numbers.
over natural numbers.
Partial Orders
A relation 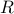 is a partial order iff it is
is a partial order iff it is
reflexive
transitive
anti-symmetric.
The easiest way to remember a partial order is to think of the 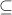 relation over sets. In fact, the partial order definition
is an abstraction of the subset relation.
relation over sets. In fact, the partial order definition
is an abstraction of the subset relation.
Example-1
Let us take the words in an english dictionary. The lexicographic ordering (or alphabetic ordering) is a partial order.
Example-2
Is the order  on
on 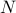 a partial order? What about the
a partial order? What about the  ordering?
ordering?
Example-3
Is the  relation on
relation on 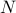 a partial order?
a partial order?
Example-4
Is the empty relation a partial order, in general?
Partial orders can leave elements incomparable. We saw the example with 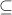 where
where
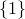 is incomparable in the
is incomparable in the 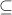 ordering to
ordering to 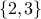 .
.
A strict partial order is an irreflexive, transitive and anti-symmetric relation.
It is inspired by the  order between sets which captures the notion of
proper subsets.
order between sets which captures the notion of
proper subsets.
Total Order
A total ordering is a partial order that also satisfies the property that there are no incomparable elements.
The definition of a total ordering is inspired by the  relation. It is a partial order over
relation. It is a partial order over 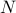 but
additionally for any
but
additionally for any 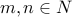 either
either 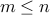 or
or 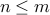 .
.
A strict total ordering is a strict partial order that ensures that no two different elements are incomparable.
Strict total orderings are inspired by the  relation on
relation on 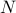 .
.
More Examples
Let us take an example and study various find of relations. Let us take the set of natural numbers and classify relations over them.
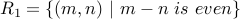 .
. 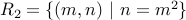 .
. 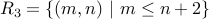 .
. 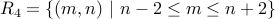 .
.
| Relation | Reflexive?? | Symmetric?? | Transitive? | Anti-Symmetric? | Irreflexive? |
| 1 | Y | Y | Y | N | N |
| 2 | N | N | N | Y | N |
| 3 | |||||
| 4 |