CSCI 2824: Lecture 27
We have two topics left over in counting/combinatorics that we will look at over the rest of this week.
Recursive Counting: counting things by establishing recurrence relations (Section 5.5 of the book)
Solving Recurrences: some basic ideas on generating functions for solving interesting recurrences (Section 5.6 of the book).
Recursive Counting
The idea behind recursive counting is to set up a recurrence that expresses what you wish to count. This is especially useful when what we wish to count does not neatly fit into any of the categories studied thus far.
Example-1
Q How many matches need to be played between  teams in a round-robin tournament?
teams in a round-robin tournament?
You should know the answer to this problem by now and be able to reason it out in many different ways.
Let us look at it recursively. Let 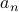 be the number of matches for
be the number of matches for  teams. We know that
teams. We know that
If
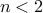 then
then 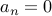 . We need at least two teams to make it interesting!
. We need at least two teams to make it interesting! Otherwise,
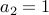 . Two teams will play exactly one match.
. Two teams will play exactly one match.
Can we now express 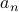 in terms of
in terms of 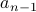 ?
?
Yes, we can say that with  teams, # of matches involving all n teams = # of matches involving teams 1… (n-1) + # of matches involving team n
teams, # of matches involving all n teams = # of matches involving teams 1… (n-1) + # of matches involving team n
Team  plays precisely
plays precisely 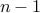 matches (one with every other team). I.e,
matches (one with every other team). I.e, 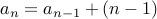 .
.
Therefore, the answer to the problem is governed by the recurrence relation:
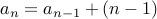 for
for 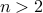
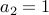 .
.
The closed form solution is indeed 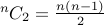 .
.
Example-2
Q What is the number of  permutations of
permutations of  objects?
objects?
In other words, what is 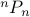 ?
?
Let us write a recurrence (in the spirit of this lecture). To obtain a permutation of  objects (numbered 1…n), let us do the following:
objects (numbered 1…n), let us do the following:
Take away the last object and permute the remaining objects from 1 .. (n-1).
After this, we can decide where to insert the last object.
Step 1 yields 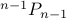 possible permutations (we pretend not to know what it may be :-) )
possible permutations (we pretend not to know what it may be :-) )
Once we have fixed a permutation of the first 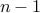 objects, there are
objects, there are  possible places where the object #n can be inserted. Therefore the recurrence is
possible places where the object #n can be inserted. Therefore the recurrence is
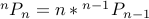
The base case for 1 object is very simple,
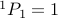 .
.
Once again, we know by eyeballing the recurrence that 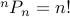 .
.
Example-3
How many solutions are there to the equation:
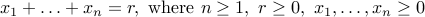 .
.
Again, let us file under the category of things we already know how to solve by different methods :-)
Let 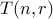 represent the answer to this problem.
represent the answer to this problem.
Simple cases:
Whenver
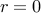 ,
, 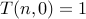 for all
for all  . There is exactly one solution (set all
. There is exactly one solution (set all 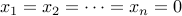 ).
). Whenever
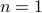 , we have just one solution. Therefore,
, we have just one solution. Therefore, 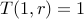 for all
for all  .
.
Recurrence. We want to count the number of solutions 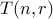 for the general case where
for the general case where 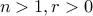 . We have two cases:
. We have two cases:
Case-1: Assume
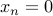 . Therefore, we can plug this in and take
. Therefore, we can plug this in and take 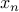 out of the system.
out of the system. This yields the system
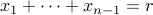 (
(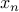 is set to zero, in other words).
is set to zero, in other words).
Case-2: Set
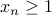 . Following standard trick we saw last friday, we can write
. Following standard trick we saw last friday, we can write 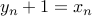 and remove
and remove 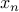 .
. This yields the system
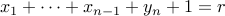 or alternatively
or alternatively 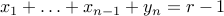 .
.
Any solution to the system either falls under case-1 or case-2. Therefore, we conclude that: 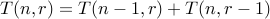 .
.
Exercise Knowing secretly that 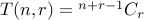 , can we verify that the recurrence holds?
, can we verify that the recurrence holds?
Example-4
We wish to roll a dice  times to obtain a sum of
times to obtain a sum of  . Each roll of
the dice can give us a number from
. Each roll of
the dice can give us a number from  to
to  .
.
Q Let 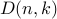 be the number of ways to obtain a sum of
be the number of ways to obtain a sum of  from
from  rolls of a dice. Write a recurrence relation for
rolls of a dice. Write a recurrence relation for 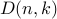 .
.
Let us get rid of the base cases.
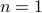 and
and 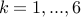 . With one roll of the dice there is just one way to obtain an outcome of
. With one roll of the dice there is just one way to obtain an outcome of 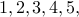 or
or 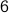 .
. 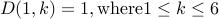 .
.
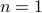 and
and 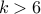 . Can you tell me what
. Can you tell me what 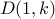 ought to be?
ought to be? 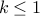 and
and 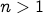 . Since we cannot turn up
. Since we cannot turn up  , we have
, we have 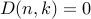 whenever
whenever 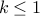 and
and 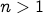 .
.
Now for the generic case. Suppose we wish to roll the dice  times and arrive at a sum of exactly
times and arrive at a sum of exactly  . Let us split cases on the last roll:
. Let us split cases on the last roll:
The last roll showed up
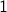 and first
and first 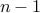 rolls sum up to
rolls sum up to 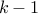 .
. The last roll shows up
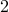 and first
and first 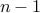 rolls sum up to
rolls sum up to 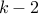

The last roll shows up to
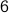 and first
and first 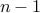 rolls sum up to
rolls sum up to 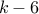 .
.
Therefore, can we now write a recurrence to express the sum?
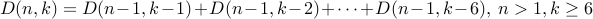 .
.
A recurrence should directly allow you to write an efficient program to compute the answer using dynamic programming.
Example-1
Let us take the following recurrence:
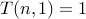 for all
for all 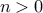
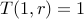 for all
for all 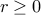
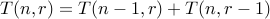 if
if 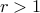 or
or 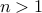 .
.
How do we solve it? We can write a program to compute 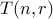 .
.
int T(int n, int r){ assert( n > 1); assert( r > 1); /*-- Base Case --*/ if ( r == 1) return 1; if ( n == 1) return 1; /* Recurrence */ return T(n-1,r) + T(n,r-1); }
I implemented this in C and ran it. Here are the running times and some results:
| n | r | Time (sec) |
| 10 | 10 | < .1 s |
| 20 | 10 | .1 s |
| 15 | 15 | .4 s |
| 17 | 17 | 6 s |
| 18 | 18 | 24 s |
| 19 | 19 | 92 s |
| 20 | 20 | 6 mins |
We will explain how this recurrence can be computed faster in class.