Discrete Structures (CSCI 2824, Spring 2014)
We will periodically post puzzles that relate to some of the material we have seen so far.
Puzzle # 1
Consider an island with two types of people: compulsive truth tellers
and compulsive liars. You arrive at a fork in the road. One path leads
to a castle and the other to a dangerous swamp. You have no idea which one.
There are two people 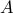 and
and 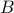 : both liars or both truth tellers.
What one question would you ask one of them to be able to deduce the right
path?
: both liars or both truth tellers.
What one question would you ask one of them to be able to deduce the right
path?
Status: Solved by Michelle S.
Ask A the question: “If I were to ask the person B the question ”which way leads to the castle?“ what would his answer be?”
Puzzle # 2
Puzzle from one of Edsger Dijkstra's papers
There are thirteen football games on a sunday and you are allowed to place a bet on the outcome of each game. Each game has one of three outcomes: 1. Team A wins, 2. Team B wins and 3. It is a tie.
If you predict the outcomes of five out of the thirteen correctly, you win a prize.
The betting company allows you to turn in a sheet with the predictions
for each of the thirteen games. You can turn in multiple sheets but
each bet costs you money.
But, if any single sheet that you submit predicts the outcomes of 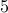 or more games correctly, you win a prize.
or more games correctly, you win a prize.
What is the minimum number of sheets that gives you a sure shot
strategy to outright win the prize, no matter what the outcomes of
the games are? Note that we are not talking probabilities of guessing
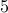 , we want a sure shot winning strategy.
, we want a sure shot winning strategy.