Proofs By Contradiction
This is also called reductio ad absurdum.
Reductio ad absurdum, which Euclid loved so much, is one of a mathematician's finest weapons. It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game
G.H. Hardy, A Mathematician's Apology, 1940.
To prove a theorem 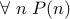 , assume that the theorem does
not hold. I.e,
, assume that the theorem does
not hold. I.e, 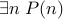 and prove that a contradiction (or
absurditity results).
and prove that a contradiction (or
absurditity results).
Consider a simple example.
Theorem For every  , If
, If 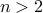 and
and  is prime then
is prime then  is odd.
is odd.
Proof We will prove by contradiction.
The original statement is
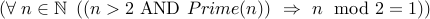
The negation of this statement is
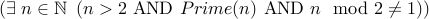
Let us assume that the original statement is false. It's negation must be true for some  . Therefore, there is a
. Therefore, there is a  such that
such that 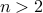 ,
,  is prime and
is prime and  is even, all at the same time.
is even, all at the same time.
Since
 is even, we can write
is even, we can write 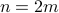 for some
for some 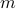 .
. Now, since
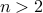 , as well,
, as well, 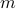 cannot be equal to
cannot be equal to 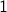 .
. As a result,
 can be written as the product of
can be written as the product of 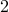 and another number
and another number 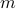 that is not
that is not 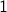 .
. Therefore,
 is composite.
is composite. However, we assumed that
 was prime.
was prime. A number cannot be prime and composite at the same time. Therefore, we have a contradiction.
Assuming the negation of the theorem leads to a contradiction. Therefore, the theorem is true.
(QED)
Proof By Contradiction
Let us look at how such proofs look like.
Universal Statement
To prove:  .
.
Assume, for the sake of contradiction, that the statement does not hold. In other words, there is a number  such that
such that
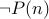 . We then use this to prove by contradiction.
. We then use this to prove by contradiction.
Universal Implication
This is a special case of universal statements.
To prove: 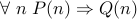 .
.
Assume, for the sake of contradiction, that the statement does not
hold. Therefore, there is a number  such that
such that 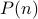 holds but
holds but
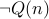 holds (or
holds (or 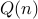 does not hold). Starting from this, we
derive a contradiction.
does not hold). Starting from this, we
derive a contradiction.
Existential Statement
To prove 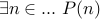 , assume that
, assume that 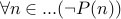 and derive the contradiction.
and derive the contradiction.
Examples of Proof By Contradiction
Here are some famous reductios.
Theorem There are infinitely many prime numbers.
Proof is by contradiction. Let us assume that there are finitely many (let us say  ) primes.
) primes.
Therefore, the prime numbers are
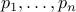 and every other number (except
and every other number (except 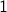 ) is composite.
) is composite. Consider the number
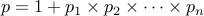 .
. We know that it is composite since the number of primes is finite and
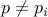 .
. We showed using strong induction that every number is divisible by some prime number.
Therefore,
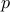 is divisible by one of
is divisible by one of 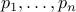 .
. However, dividing
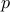 by
by 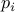 leaves a remainder of
leaves a remainder of 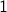 for each
for each 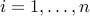 .
. As a result, we conclude that
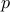 is a prime too.
is a prime too.
This means that
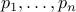 cannot be all the primes.
Therefore, we have a contradiction.
cannot be all the primes.
Therefore, we have a contradiction.
Here is another one from Euclid.
Theorem The number 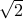 is irrational.
is irrational.
Proof is again by contradiction. Let us assume that
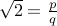 for integers
for integers 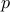 and
and 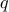 . We also assume that
. We also assume that
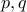 are at their lowest terms. In other words,
are at their lowest terms. In other words, 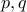 have no common
factors.
have no common
factors.
We know that 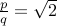 . Therefore,
. Therefore, 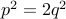 .
.
This means that
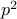 is even. Therefore,
is even. Therefore, 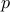 is even.
is even. However,
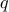 cannot be even since
cannot be even since  would then not be in their lowest terms.
would then not be in their lowest terms. Therefore,
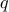 is odd.
is odd.Since
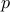 is even, we can write
is even, we can write 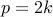 . Therefore
. Therefore 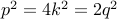 .
. We conclude that
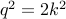 . In other words,
. In other words, 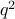 is even and hence
is even and hence 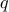 is even.
is even.
This is a contradiction since 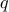 cannot be odd and even at the same time. QED.
cannot be odd and even at the same time. QED.