Pigeon Hole Principle
The basic principle is very simple:
If there are  pigeons and
pigeons and 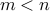 holes to put those pigeons in, then at least two pigeons need to be
put in the same hole.
holes to put those pigeons in, then at least two pigeons need to be
put in the same hole.
Even this simple principle can help prove some very surprising results.
Example-1
Imagine a party with 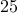 guests. Assume that everyone in the party knows at least one other person but is a stranger to at least one other person.
There are at least two people who know the same number of people.
guests. Assume that everyone in the party knows at least one other person but is a stranger to at least one other person.
There are at least two people who know the same number of people.
Example-2
Zip is a commonly used compression algorithm. We know that zip can compress most files. By pigeon hole principle we can conclude that there is at least one file that zip will not compress (expand).
Example-3
Sequential circuit output:
A Boolean circuit has three LEDs at its output that can either glow red or green depending on the input. It has 4 Boolean input wires and for each input, it has a specific patterns for output LEDs. Show that there are at least two inputs for which the output pattern will be the same.
Extended Pigeon Hole Principle
If there are 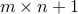 objects to be distributed in
objects to be distributed in  bins, then at least one bin has more than
bins, then at least one bin has more than 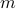 objects.
objects.
Example-1
This class has 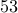 students attending on average. I can confidently
say that at least two of you will have a birthday that falls on the
same week.
students attending on average. I can confidently
say that at least two of you will have a birthday that falls on the
same week.
In fact, at least 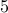 of you will have a birthday that falls on the same month. How can I say these statements without knowing your
birthdays? :-)
of you will have a birthday that falls on the same month. How can I say these statements without knowing your
birthdays? :-)
Assuming all of you hail from somewhere in the USA, I happen to know that at least two of you are from the same state. :-)
Example-2
Sequential circuit output: A Boolean circuit has three LEDs at its output that can either glow red or green depending on the input. It has 5 Boolean input wires and for each input, it has a specific patterns for output LEDs.
We can now show that there are at least 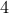 inputs that produce the same output.
inputs that produce the same output.
Pigeon Hole Principle to Prove Properties of Numbers
Theorem Whenever 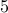 points are placed inside a
points are placed inside a 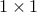 square at least two will be within a distance of less than
square at least two will be within a distance of less than 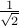 .
.
Proof We need to draw a picture of a square and divide it into four equal squares of size 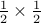 each. By PH principle,
at least two of the points will be on the same small square. The longest distance these two points can be apart inside the small square is the length
of its diagonal.
each. By PH principle,
at least two of the points will be on the same small square. The longest distance these two points can be apart inside the small square is the length
of its diagonal.
Draw picture in class
Theorem Whenever 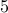 points are placed on the circumference of a circle with center
points are placed on the circumference of a circle with center 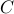 , there will be at least two points
, there will be at least two points 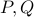 with the angle
with the angle 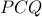 being acute.
being acute.
Proof Again divide the circle into four quadrants. Two of the points have to lie on the same quadrant by pigeon hole principle.
Draw picture in class
Theorem Whenever five points are placed on the surface of a sphere, the sphere can be cut into two halves (hemispheres) such that four points are on one half.
Draw picture in class
Ramsey's Theorem
Ramsey's theorem is a very cool fundamental fact of combinatorics. It has many (equivalent) flavors:
In any class of six or more people, there are at least three mutual friends or three mutual strangers.
Take 6 points that form the corners of a 6 sided figure and between every two points either draw a red line or a green line. Then there has to be a red triangle or a green triangle.
Any graph
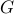 with
with 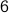 nodes has a
nodes has a 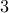 -clique or a
-clique or a 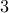 -independent set.
-independent set. Ramsey Number (3,3) = 6.
and so on.
We will prove this theorem in class.