Lecture Ten Notes
In this lecture we will talk further about induction: including strong induction, the need to strengthen the statements for induction and talk about induction over programs.
This lecture corresponds to section 2.3 of Ensley and Crawley's book. Some of the material is not available in Ensley-Crawley. Please refer to these notes.
The General (Strong) Induction.
Fallacies with Strong Induction.
Induction on Programs
Strong Induction
To prove a statement 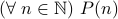 by strong induction.
by strong induction.
Base Case: Establish
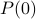 (or in general the smallest number for which the theorem is claimed to hold.).
(or in general the smallest number for which the theorem is claimed to hold.). Inductive hypothesis: For all
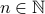 , Assuming
, Assuming  hold, prove
hold, prove 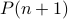 .
.
Strong induction is the “mother” of all induction principles. We can formulate many “baby” induction principles that are all just restatements of strong induction. In fact, mathematically they are all the same principle in different guises. However, seeing that is a little beyond the scope of this class.
Weak Induction
To prove a statement 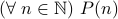 by weak induction.
by weak induction.
Base Case: Establish
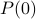 (or in general the smallest number for which the theorem is claimed to hold.).
(or in general the smallest number for which the theorem is claimed to hold.). Inductive hypothesis: For any
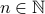 , assuming
, assuming 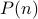 holds, prove
holds, prove 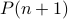 .
.
Step-By-Two Induction
To prove a statement 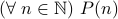 by step-by-two induction.
by step-by-two induction.
Base Case: Establish
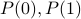 (or in general the smallest number and its successor).
(or in general the smallest number and its successor). Inductive hypothesis: Assuming
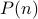 holds, prove
holds, prove 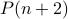 .
.
Q: Why does step-by-two induction need two base cases?
Look-Back-By-Two Induction
To prove a statement 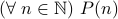 by Look-Back-By-Two induction.
by Look-Back-By-Two induction.
Base Case: Establish
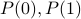 (or in general the smallest number and its successor).
(or in general the smallest number and its successor). Inductive hypothesis: For
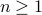 , assuming
, assuming 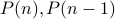 holds, prove
holds, prove 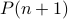 .
.
Q: Why does look-back-by-two induction need two base cases?
Step-By-Three Induction
To prove a statement 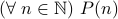 by step-by-three induction.
by step-by-three induction.
Base Case: Establish
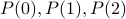 (or in general the smallest number and its next two successors).
(or in general the smallest number and its next two successors). Inductive hypothesis: Assuming
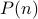 holds, prove
holds, prove 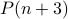 .
.
Q: Why does step-by-three induction need three base cases?
We can continue with a cottage industry that produces induction principles, but we will stop here!
Why Strong Induction?
Let us try to prove a couple of theorems that will require strong induction.
Theorem-1: Every number 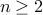 is divisible by a prime number.
is divisible by a prime number.
We will attempt prove by weak induction first.
Base Case: This holds for
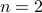 , which is a prime number and is divisible by itself.
, which is a prime number and is divisible by itself. Induction Hypothesis: If
 is divisible by a prime number then so is
is divisible by a prime number then so is 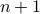 . The difficulty of proving this should be clear. Knowing something about divisibility of
. The difficulty of proving this should be clear. Knowing something about divisibility of 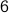 does not let us conclude the divisibility for
does not let us conclude the divisibility for 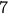 .
.
Proof Failed
We will now try strong induction.
Base Case: This holds for
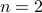 .
. Induction Hypothesis: Assume that
 hold for any
hold for any 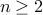 and prove that
and prove that 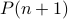 holds.
holds.
Notes: (a) 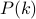 here means
here means  is divisible by a prime number. (b) The theorem only applies for
is divisible by a prime number. (b) The theorem only applies for 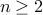 . We can start induction from there.
. We can start induction from there.
Let us assume that for all 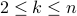 ,
,  is divisible by a
prime number. We wish to prove that
is divisible by a
prime number. We wish to prove that 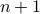 is divisible by a prime
number. Since
is divisible by a prime
number. Since 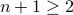 , we know that
, we know that 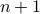 is either prime or composite.
We are allowed to split two cases:
is either prime or composite.
We are allowed to split two cases:
Case-1
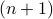 is a prime number itself. So in this case, it is trivially divisible by itself.
is a prime number itself. So in this case, it is trivially divisible by itself. Case-2
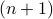 is composite. Therefore there is a number
is composite. Therefore there is a number 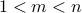 such that
such that 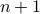 is divisible by
is divisible by 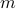 .
.
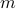 is divisible by some prime
is divisible by some prime 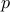 , by induction hypothesis.
Therefore
, by induction hypothesis.
Therefore 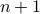 is divisible by some prime
is divisible by some prime 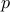 .
.
QED
Faulty Applications of Induction
Miss out on the base case(s).
Claim: Every number 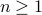 is odd.
is odd.
Base Case: We know that
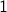 is odd. So base case is verified.
is odd. So base case is verified.
Induction Hypothesis: Assuming that all numbers
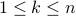 are odd, we wish to prove that
are odd, we wish to prove that 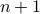 is also odd.
is also odd.Let us assume all numbers
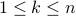 are odd.
are odd. We wish to prove that
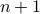 is odd.
is odd. By induction hypothesis,
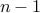 is odd.
is odd. Therefore
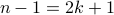 for some
for some  .
. Therefore, we conclude that
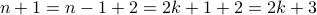 .
. Therefore,
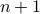 is also odd.
is also odd.
QED??
The proof failed because the Induction hypothesis proof is flawed. Let us split the proof step by step.
Induction Hypothesis:
Let us assume that all numbers
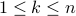 are odd. ( Perfectly within your rights to assume because of the strong induction )
are odd. ( Perfectly within your rights to assume because of the strong induction )We wish to prove that
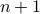 is odd. ( good luck! )
is odd. ( good luck! )By induction hypothesis
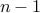 is odd. ( Wait a minute, this does not work for
is odd. ( Wait a minute, this does not work for 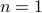 . For
. For 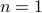 , we have
, we have 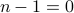 which falls outside the scope of the induction hypothesis! ) FAIL!!
which falls outside the scope of the induction hypothesis! ) FAIL!!
Here is a funny version of the same proof.
Claim: All horses are of the same color.
Proof by weak induction on number of horses.
Base case: Any single horse is of the same color as itself.
Induction: Let us assume that for every set of
 horses have the same color.
horses have the same color. We wish to prove the same for a set of
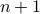 horses.
horses. Let us take any set of
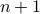 horses and call them
horses and call them 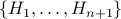 .
. We can split the set into two parts
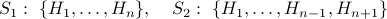
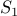 has
has  horses in it. By induction hypothesis, they all have the same color.
horses in it. By induction hypothesis, they all have the same color.Again
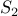 is a set of
is a set of  horses. So they all have the same color.
horses. So they all have the same color.How do we know that
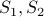 both have the same color. Becase they have horses
both have the same color. Becase they have horses 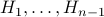 in common.
in common.Therefore
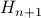 must have the same color as
must have the same color as 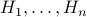 .
.
All set of
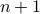 horses have the same color.
Ergo, all horses indeed have the same color.
horses have the same color.
Ergo, all horses indeed have the same color.
The flaw behind this failed proof was explained in this class.
Application: Divisibility Test for Binary Numbers
In the very first lecture, we derived a divisibility test for binary number division by 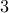 . As part of that
test, we claimed the following theorem:
. As part of that
test, we claimed the following theorem:
Theorem: For all natural numbers  ,
, 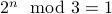 if
if  is even and
is even and 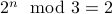 if
if  is odd.
is odd.
Proof is by step-by-two induction on  .
.
Base Cases We verify that for 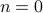 , we have
, we have 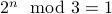 and likewise, for
and likewise, for 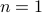 , we have
, we have 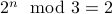 .
.
Induction-Hypothesis (Step by Two) For any  , assume that
, assume that
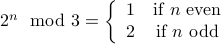 ,
,
we wish to prove that for 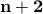 ,
,
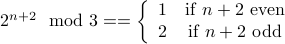 .
.
Proof of I.H. Let  be any given number such that
be any given number such that
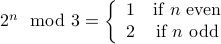
Consider 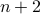 . We have
. We have 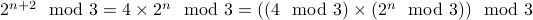 .
.
Therefore, 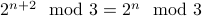 . Thus, if the property holds for
. Thus, if the property holds for  it also holds for
it also holds for 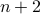 .
.
This same proof can be done by strong induction or even weak induction, if you wish.
Inductive proofs of programs
Often, we are interested in proving that a program we wrote is correct. For instance, let us take a simple program that adds the elements of an array to find the total. We wish to prove that it is correct.
def sumArray(a,n): # Assume a is an array of size n # Assume n > 0 # Array elements are a[0]..,a[n-1] sum = 0 j = 0 while (j < n): # LOOP HEAD sum = sum + a[j] j = j +1
We note that whenever we reach the loop head, the following facts always hold:
(A) 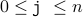 (The value of j remains between 0 and n )
(The value of j remains between 0 and n )
(B) ![mbox{texttt{sum}} = sum_{i=0}^{mbox{texttt{j-1}}} a[i]](eqs/6830760370739889587-130.png) (The value of sum is the partial sum of the first j-1 array elements ).
(The value of sum is the partial sum of the first j-1 array elements ).
These facts are called loop invariants. Establishing a loop invariant is a fundamental task in proving that a program is correct.
A condition involving the program variables is a loop invariant if it is true whenever the LOOP HEAD is reached.
Let us try to state the loop invariant as a theorem involving the sumArray program.
Theorem Whenever control reaches LOOP HEAD the value of j satisfies the condition 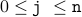 .
.
Proof is by weak induction on the number of times 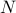 the loop body
has been executed. We use
the loop body
has been executed. We use 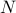 here to distinguish it from
here to distinguish it from 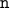 the program variable.
the program variable.
Base Case:
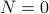 . This corresponds to the very first time, the loop is reached. We know by looking at the program that
. This corresponds to the very first time, the loop is reached. We know by looking at the program that 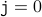 . This satisfies the property
. This satisfies the property 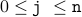 , since we are given that
, since we are given that 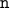 is the size of array
is the size of array  which cannot be negative.
which cannot be negative.
Induction Hypothesis:
Let us assume that the property holds after 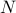 executions of the
loop body. We wish to prove that it holds after
executions of the
loop body. We wish to prove that it holds after 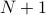 executions.
executions.
Let 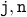 be values of the variables at the loop head after the loop has been executed
be values of the variables at the loop head after the loop has been executed 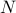 times.
We assume that the inductive hypothesis holds. In other words,
times.
We assume that the inductive hypothesis holds. In other words, 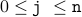 is true. We wish to prove that if we execute the loop body once more, the resulting values for the variables
is true. We wish to prove that if we execute the loop body once more, the resulting values for the variables
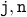 will also satisfy the invariant.
will also satisfy the invariant.
Since
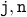 are such that the loop can be executed
one more time, it must be the case that
are such that the loop can be executed
one more time, it must be the case that 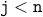 must
be true.
must
be true. After the loop is executed, we have
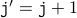 and
and 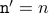 where the prime ’ next to the
variables are used to separate the values after the loop is executed
once from the values before.
where the prime ’ next to the
variables are used to separate the values after the loop is executed
once from the values before.We therefore have that if
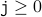 then
then 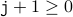 .
. Similarly, since
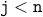 (due to the loop condition), we have
(due to the loop condition), we have 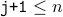 .
.
Together, we have 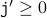 and
and 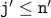 . Thus, the loop condition holds even after the loop has been
executed once.
. Thus, the loop condition holds even after the loop has been
executed once.
Let us now prove the loop invariant property of partial sums for the loop:
![mbox{texttt{sum}} = sum_{i=0}^{mbox{texttt{j-1}}} a[i]](eqs/6830760370739889587-130.png)
Note that 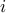 here is the index variable of the summation notation
here is the index variable of the summation notation  and not a
program variable.
and not a
program variable.  on the other hand, is very much a
program variable.
on the other hand, is very much a
program variable.
Theorem Whenever the control reaches LOOP-HEAD, we have
![mbox{texttt{sum}} = sum_{i=0}^{mbox{texttt{j-1}}} a[i]](eqs/6830760370739889587-130.png)
Once again, we prove by induction on 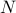 , the number of times the loop has been executed.
, the number of times the loop has been executed.
Base-Case For 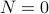 , we have that the loop body has never been executed. Therefore,
, we have that the loop body has never been executed. Therefore,
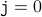 and
and 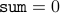 . We therefore have
. We therefore have
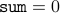
![sum_{i=0}^{mbox{texttt{j-1}}} a[i] = underset{mbox{empty summation is zero}}{underbrace{sum_{i=0}^{-1} a[i]}} = 0](eqs/5292258246319109226-130.png)
Therefore, we conclude that
![mbox{texttt{sum}} = sum_{i=0}^{mbox{texttt{j-1}}} a[i]](eqs/6830760370739889587-130.png)
Ind.Hyp. Assume that the property holds after N loop executions, we wish to prove that it holds after N+1 loop executions.
Let  be the values of the
corresponding variables after the loop has executed
be the values of the
corresponding variables after the loop has executed 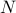 times. We
assume that the loop executes one more time and gives us the values
times. We
assume that the loop executes one more time and gives us the values
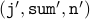 . Examining the loop, we
conclude the following relevant facts:
. Examining the loop, we
conclude the following relevant facts:
Assuming the induction hypothesis, we have
![begin{array}{rcll} texttt{sum}' &=& texttt{sum} + a[texttt{j}] & textcolor{red}{mbox{(From loop body )}} &=& sum_{i=0}^{mbox{texttt{j-1}}} a[i] + a[texttt{j}] &textcolor{red}{mbox{(From I.H for texttt{sum} )}} &=& sum_{i=0}^{mbox{texttt{j}}} a[i] & textcolor{red}{mbox{(Last term is pushed into the summation)}} &=& sum_{i=0}^{mbox{texttt{j}'-1}} a[i] & textcolor{red}{(mbox{substitute} texttt{j}' = texttt{j} + 1 )} end{array}](eqs/8072871898312411787-130.png)
In other words, we have established that
![texttt{sum}' = sum_{i=0}^{mbox{texttt{j}'-1}} a[i]](eqs/277765499456216842-130.png)
QED
To understand the value of inductive invariants, can you explain how the proof will fail if the program were modified slightly as
def sumArray(a,n): # Assume a is an array of size n # Assume n > 0 # Array elements are a[0]..,a[n-1] sum = 0 j = 0 while (j < n): # LOOP HEAD j = j +1 # Fault: incrementing j first and then adding sum = sum + a[j] # Fault: buffer overflow possible
Program to compute logarithm
We now consider a program that given a number 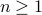 , returns
a number
, returns
a number  such that
such that 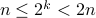 . In other words
. In other words 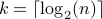 .
.
def logtwo(n): # Assume n >= 1 lg = 0 j = 1 while (j < n): # LOOP HEAD lg = lg +1 j = j *2 return lg
Please take a second to understand how the program works. You can try it in a python interpreter.
To prove that this program is correct, we will provide the following loop invariants for the while loop.
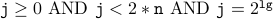
Proof is by induction on 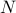 , the number of steps the while loop is executed.
, the number of steps the while loop is executed.
Base Case For 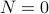 , we know that
, we know that 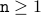 ,
, 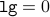 and
and 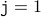 . We are also assuming that
. We are also assuming that 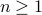 .
.
Therefore, it is easy to check that the invariant
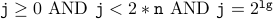
is satisfied.
I.H If the loop invariant is true after the loop has been executed 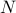 times then it remains true after the loop has been executed
times then it remains true after the loop has been executed 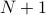 times.
times.
Again, let us assume the loop has been executed 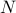 times and
times and
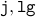 and
and 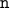 be the values for these
variables. Let us assume that the loop executes one more time and the
resulting values are
be the values for these
variables. Let us assume that the loop executes one more time and the
resulting values are 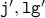 and
and 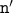 .
.
Here is a summary of the facts we know about these:
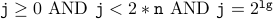 (from the induction hypothesis )
(from the induction hypothesis )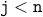 ( because, the loop condition should be satisfied )
( because, the loop condition should be satisfied )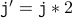 ( body of the loop )
( body of the loop )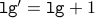
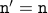 .
.
Let us now prove that
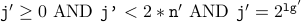 going conjunct by conjunct.
going conjunct by conjunct.
(a) Proof of 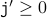
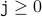 (from the induction hypothesis )
(from the induction hypothesis )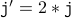 ( body of the loop )
( body of the loop )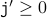 .
.
(b) Proof of 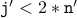
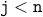 ( because, the loop condition should be satisfied )
( because, the loop condition should be satisfied )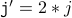 ( body of the loop )
( body of the loop )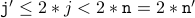 ( chaining the inequalities together )
( chaining the inequalities together )
(c) Proof that 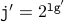 .
.
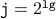 (from the induction hypothesis )
(from the induction hypothesis )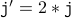 ,
, 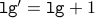 ( body of the loop )
( body of the loop )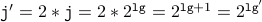 .
.
Therefore, we have proved that
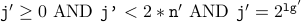
Now, it remains to put together the inductive invariant to prove the the log function “works”.
Note that the while loop finishes when 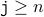 (the negation of the loop condition holds).
However, if the control is at the LOOP-HEAD the loop invariant holds.
(the negation of the loop condition holds).
However, if the control is at the LOOP-HEAD the loop invariant holds.
Therefore, we have the following facts:
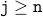
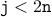
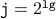 .
.
Putting them together, we conclude that when the loop terminates,
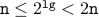 .
.
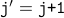
![texttt{sum}' = texttt{sum} + a[texttt{j}]](eqs/5424277553480892231-130.png)