CSCI 2824: Lecture 28
In this lecture, we will look at the following topics:
Walks, Paths, and Cycles (revision}
Connectedness and Connected Components.
Bipartite Graphs.
Colorability of Graphs.
We will start by revising walks, paths and give examples.
Walks
Let 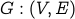 be a directed graph with vertices
be a directed graph with vertices 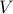 and edges
and edges 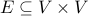 .
.
A walk over  is a sequence of vertices and edges:
is a sequence of vertices and edges:
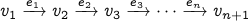
where
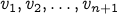 are vertices visited during the walk.
are vertices visited during the walk.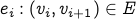 , for
, for ![i in [1,n]](eqs/3953253595448023572-130.png) .
.
In other words, a walk over a graph is simply a sequence of visits to vertices and edges of the graph wherein
We may start anywhere in the graph.
A single step of the walk consists of taking an outgoing edge from the current vertex
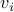 to visit a vertex
to visit a vertex 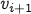 .
. We end after a finite but arbitrary number of steps.
Example-1
Take the graph:
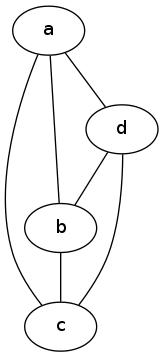
Here are some walks
 (just start and stop at
(just start and stop at  ).
). 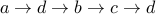 .
. 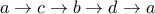 .
.
Paths
Simply stated a path between two nodes 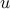 and
and  (where
(where 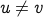 ) is a walk that
) is a walk that
begins at
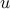 ,
, ends at
 ,
, No vertex is repeated, i.e, each vertex is visited at most once.
The length of a path is the number of edges in it.
Example-1
Take the graph:
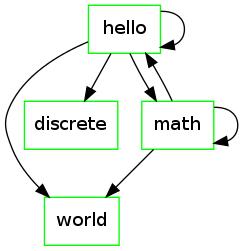
There are two paths between 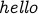 and
and 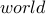 :
:
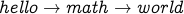 (path of length 2).
(path of length 2). 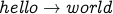 (path of length 1).
(path of length 1).
The following are not paths:
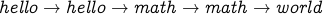 .
. 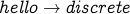 .
In the first case,
.
In the first case, 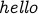 (and
(and 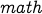 ) are repeated vertices which is not allowed.
In the second case, the path does not end in
) are repeated vertices which is not allowed.
In the second case, the path does not end in 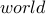 , rather it ends in
, rather it ends in 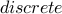 .
.
Example-2
Consider the undirected graph 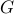 :
:

There are at least five paths from  to
to 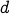 :
:
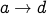 (length is 1).
(length is 1). 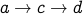 (length is 2).
(length is 2). 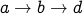 (length is 2).
(length is 2). 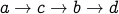 (length is 3).
(length is 3). 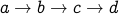 (path length is 3).
(path length is 3).
Are there any more paths between  and
and 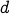 ?
?
Note that even though the graph is undirected, the path itself is from  to
to 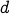 . However, since the graph
is undirected, we note that any path from
. However, since the graph
is undirected, we note that any path from  to
to 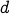 may be reversed to immediately yield a path from
may be reversed to immediately yield a path from 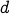 to
to  .
.
This is not always true in a directed graph. In the previous example there is a path from 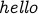 to
to 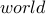 but
not vice-versa.
but
not vice-versa.
Cycle
A cycle in a graph is a “path” from a vertex back to itself. I place “path” under quotes because we just defined paths so that vertices cannot repeat.
Formally, a cycle is a sequence of nodes and edges of the form
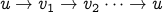
where other than 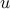 itself no vertex or edge can repeat.
itself no vertex or edge can repeat.
The length of a cycle is the number of edges in it.
The choice of a starting point in a cycle is arbitrary in the following sense. We could have written the same cycle above as
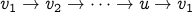
Example-1
Take the graph:

Examples of cycles in this graph include:
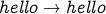 (self loop = length 1 cycle).
(self loop = length 1 cycle). 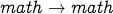
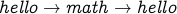 which is the same cycle as
which is the same cycle as 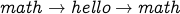 (the cycle has length 2).
(the cycle has length 2).
Example-2
Consider the following undirected graph instead:
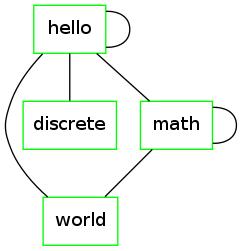
Note that 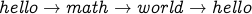 is a cycle in this graph of length
is a cycle in this graph of length 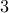 .
.
The direction of a cycle does not matter in an undirected graph. The same cycle may be written as
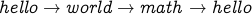 .
.
Important Note 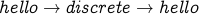 is not considered a cycle in the undirected
graph. The reason is that the undirected edge
is not considered a cycle in the undirected
graph. The reason is that the undirected edge 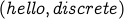 and
and 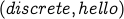 are
considered the same edge for the undirected graph and is being traversed twice.
In other words, a cycle cannot repeat an edge.
are
considered the same edge for the undirected graph and is being traversed twice.
In other words, a cycle cannot repeat an edge.
Connected Components
We will discuss connected components for undirected graphs. The definition for directed graph is possible but is a little harder to understand.
Many books also call connected components as strongly connected components.
Basic Idea
Let us start with the following example over the set of vertices:  .
.
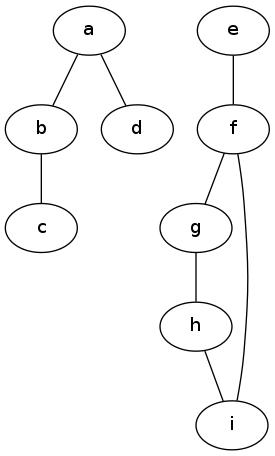
The graph has two “islands”:  and
and 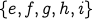 . There is no path from any vertex
in the second island to the first “island”. The term island is imprecise. The concept
of a connected component is useful here.
. There is no path from any vertex
in the second island to the first “island”. The term island is imprecise. The concept
of a connected component is useful here.
We say that a subset of vertices 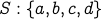 is a connected component of a graph
is a connected component of a graph 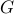 . I.e., if you
choose any pair of vertices in the set then there is a path between them that just involves the vertices
in the set
. I.e., if you
choose any pair of vertices in the set then there is a path between them that just involves the vertices
in the set 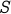 .
.
By the same token, the set 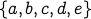 is not a connected component. Since there is no path from
is not a connected component. Since there is no path from  to
to 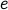 (since
it is an undirected graph, there is no path from
(since
it is an undirected graph, there is no path from 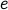 to
to  either).
either).
Also the set 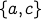 is not a connected component since the only possible path in
is not a connected component since the only possible path in 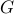 from
from  to
to  has to pass through
has to pass through 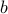 which is not included in the set.
which is not included in the set.
Definition
Let 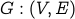 be an undirected graph. Let us take a subset of vertices
be an undirected graph. Let us take a subset of vertices 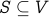 .
.
We say that 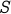 is a connected component (also often called a strongly connected component) iff the following hold:
is a connected component (also often called a strongly connected component) iff the following hold:
for any two vertices
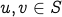 , if
, if 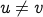 then there is a path in
then there is a path in 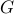 from
from 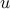 to
to 
the path involves only those vertices that appear in
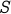 (in other words, we cannot have the path use a vertex outside the set
(in other words, we cannot have the path use a vertex outside the set 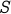 ).
).
A connected component 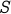 is called a maximal connected component if for every vertex
is called a maximal connected component if for every vertex 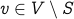 ,
, 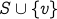 is not a connected component.
is not a connected component.
In other words, adding any new vertex to the component destroys its connectivity.
Example
Consider the graph 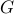 below:
below:

| Set | Connected Component? | Maximal Connected Component | Remarks |
| {a,b} | Yes | No | The addition of 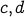 makes it maximal makes it maximal |
| {e,i,g} | No | No | The path from e to i has to involve either f or h which are both not in the set |
| {a,b,c,d} | Yes | Yes | Adding any other vertex to the set stops it from being a conn. comp. |
| {e,f,g,h,i} | Yes | Yes | Again same as previous example |
| {a,b,c,d,e,f,g,h,i} | No | No | No path from  to to 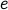 |
| {a} | Yes | No | By our definition any empty or singleton set is a connected component vacuously |
Connected Component for Directed Graphs
For directed graphs, the definition is almost the same.
Let 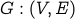 be a directed graph.
be a directed graph.
A subset 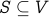 of the vertices is a connected component of a directed graph
of the vertices is a connected component of a directed graph 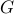 iff
iff
for any pair of vertices
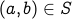 , there is a path from
, there is a path from  to
to 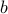 and also a path from
and also a path from 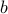 to
to  .
.both paths can only involve vertices in the set
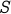 .
.
We will not look at this concept any further for now. You will encounter this in your Algorithms class (you will be shown an algorithm to compute the CCs of a graph using depth-first search).
Bipartite Graphs
Bipartite comes from bi meaning two and partite meaning partitioned into.
A graph 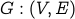 (may be directed or undirected) is bipartite iff the vertex set
(may be directed or undirected) is bipartite iff the vertex set 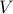 can be partitioned into two
disjoint parts
can be partitioned into two
disjoint parts 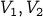 where
where
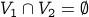 and
and 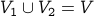 , and
, andany edge in the graph goes from a vertex in
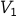 to a vertex in
to a vertex in 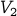 or vice-versa.
or vice-versa.
In other words, there can be no edges between vertices in 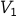 or no edges between vertices in
or no edges between vertices in 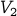 .
.
Often, we think of bipartite graphs as two colorable graphs. I.e, it is possible to assign one of two different colors to the nodes of the graph so that every edge connects nodes of different color (and no edge connects nodes of the same color).
It is easy to see that any bipartite graph is two colorable and
vice-versa. Simply take the set 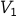 and color it red and color the
set
and color it red and color the
set 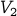 green. Likewise, if the graph can be colored using two
colors, define
green. Likewise, if the graph can be colored using two
colors, define 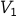 as the red colored nodes and
as the red colored nodes and 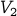 as the green
nodes.
as the green
nodes.
Example
Here is an example bipartite graph  :
:
The subset  is denoted by red squares
is denoted by red squares 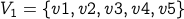 . The remaining nodes are in subset
. The remaining nodes are in subset  .
Note that any edge goes between these subsets. There are no edges between nodes of the same partition.
We can draw the same bipartite graph in a better way to bring out its bipartiteness:
.
Note that any edge goes between these subsets. There are no edges between nodes of the same partition.
We can draw the same bipartite graph in a better way to bring out its bipartiteness:
Bipartite Graphs and Cycles
We now state the key results involving bipartite graphs.
A graph 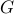 is bipartite if and only if it has no odd length cycles
is bipartite if and only if it has no odd length cycles
The theorem has two parts to it:
Any graph with an odd length cycle cannot be bipartite.
Any graph that does not have odd length cycles must be bipartite.
Odd Length Cycles 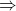 Not Bipartite.
Not Bipartite.
It is easy to show that a cycle of odd length cannot occur in a bipartite graph. Let us first just take a graph that is itself a single cycle.
An interesting pattern emerges:
| n | Bipartite? |
| 2 | Yes |
| 3 | No |
| 4 | Yes |
| 5 | No |
| 6 | Yes |
| 7 | No |
| 2k | Yes |
| 2k+1 | No |
All odd cycles cannot be two colored, whereas even cycles can. Therefore, we note a key observation.
If a graph has an odd cycle someplace inside it, no assignment of two colors will work. This is because the odd cycle cannot be two colored.
This proves that a bipartite graph cannot have an odd length cycle inside.
Not bipartite  odd length cycle.
odd length cycle.
This direction is slightly more complex.
Assume the graph is connected. Otherwise, will prove this separately for each maximally connected component of the graph.
Choose an arbitrary start node  and make two sets
and make two sets
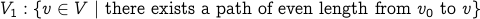
and

It is easy to prove that if the graph is bipartite, then 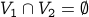 , and coloring every node in
, and coloring every node in 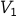 as 'White’ and
coloring every node in
as 'White’ and
coloring every node in 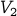 as black will provide a partition of the graph.
as black will provide a partition of the graph.
Otherwise, if the graph is not bipartite, then 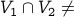 . Therefore, there exists a node
. Therefore, there exists a node  that is reachable from
that is reachable from
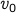 by an even length path and an odd length path.
by an even length path and an odd length path.
Therefore, there is a walk of odd length starting at 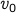 and ending
in
and ending
in 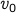 obtained by combining the odd and even length paths from
obtained by combining the odd and even length paths from 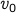 to
to  .
.
We can use a well known result that any walk of odd length from 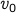 to
to 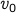 in a graph
has an odd length cycle.
in a graph
has an odd length cycle.
We will write a simple program that performs a depth-first search, and will try to color the nodes of a graph black and white in an alternating fashion, while performing a depth first search.
# Main function that visits a node v and seeks to color it with colorID # It perfoms a depth first search starting from v to color successors with the opposite color. # If it finds a that a node has been colored white and then black, then it reports a CONFLICT def colorNode(G,v,colorID): # Have I already seen node v before? if (alreadyVisitedNode(v)): if (colorNode(v) is not colorID): raise 'CONFLICT' # EXIT: the graph is NOT bipartite else: return # Nothing else to be done. # Mark that node v has been visited markVisited(v) succColor = complement(colorID) # Iterate through all outgoing nodes and # color them with opposite (complement) color foreach u in adjacency(v): colorNode(G,v, succColor) #MAIN LOOP # just start off by coloring every node that has not been # already visited with the White color. # foreach vetex v in G: if (not alreadyVisitedNode(v)): colorNode(G,v,'White')
A graph is not bipartite if and only if the function 'colorNode’ returns a 'CONFLICT’. Otherwise, the procedure will color the graph successfully with two colors showing that it is bipartite.
You should be able to use your data structures know-how to easily write code that given a graph says whether or not it is bi-partite.