Lecture 18 : One-to-One and Onto Functions.

In this lecture, we will consider properties of functions:

Functions that are One-to-One, Onto and Correspondences.
- Proving that a given function is one-to-one/onto.
Comparing cardinalities of sets using functions.

One-to-One/Onto Functions

Here are the definitions:

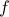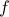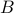is one-to-one (injective) if maps every element of to a unique element in . In other words no element of 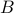are mapped to by two or more elements of .
- .
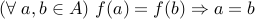is onto (surjective)if every element of 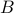is mapped to by some element of . In other words, nothing is left out.
- .
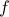is one-to-one onto (bijective) if it is both one-to-one and onto. In this case the map 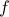is also called a one-to-one correspondence.

Example-1

Classify the following functions 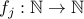$f_j: mathbb{N} rightarrow mathbb{N}$ between natural numbers as one-to-one and onto.

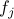	One-to-One?	Onto?
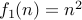	Yes	No
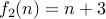	Yes	No
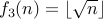$f_3(n) = lfloor sqrt{n} rfloor$	No	Yes
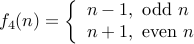$f_4(n) = left{begin{array}{l} n-1, mbox{odd} n n+1, mbox{even} n end{array} right.$ .	Yes	Yes

It helps to visualize the mapping for each function to understand the answers.

Reasons

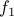is not onto because it does not have any element such that 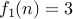, for instance.
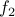is not onto because no element such that 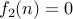, for instance.
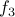is not one-to-one since .

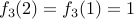Example-2

Prove that the function 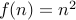f(n) = n^2 is one-to-one.

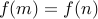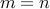Proof: We wish to prove that whenever f(m) = f(n) then m=n . Let us assume that 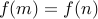for two numbers 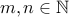m,n in mathbb{N} . Therefore, 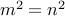m^2 = n^2 . Which means that 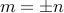m = pm n . Splitting cases on , we have

For 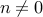, , 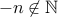therefore 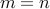for this case.
For 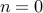, we have 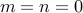. Therefore, it follows that 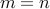for both cases.

Example-3

Prove that the function 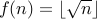f(n) = lfloor sqrt{n} rfloor is onto.

Proof

Given any 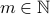m in mathbb{N} , we observe that 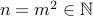$n = m^2 in mathbb{N}$ is such that 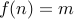f(n) = m . Therefore, all 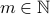are mapped onto.

Claim-1 The composition of any two one-to-one functions is itself one-to-one.

Proof

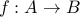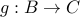Let f: A rightarrow B and g: B rightarrow C be both one-to-one. We wish to tshow that 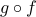g circ f is also one-to-one.

Assume that 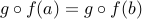for two elements .
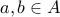Therefore .
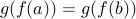Since 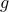is itself one-to-one, it follows that .
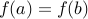Since 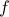is one to one and 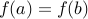it follows that .
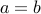Therefore 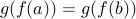can happen only if .

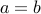The reasoning above shows that 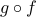gcirc f is one-to-one.

Claim-2 The composition of any two onto functions is itself onto.

Proof

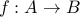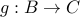Let f: A rightarrow B and g: B rightarrow C be onto functions. We will prove that 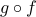g circ f is also onto.

Let 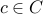be any element.
Since 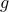is onto, we know that there exists 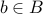such that .
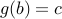Likewise, since 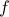is onto, there exists 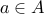such that .
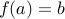Combining, .
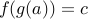Thus, 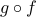is onto.

Comparing Cardinalities of Sets

Let and 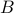be two finite sets such that there is a function 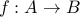f: A rightarrow B . We claim the following theorems:

If 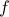is one to one then .
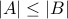If 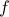is onto then .
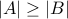If 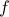is both one-to-one and onto then .

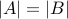The observations above are all simply pigeon-hole principle in disguise.

Theorem Let 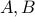A,B be two finite sets so that 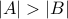|A| > |B| . Any function from to 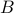cannot be one-to-one.

Proof

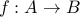Let f: A rightarrow B be any function. Think of the elements of 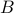as the holes and elements of as the pigeons. There are more pigeons than holes. Therefore two pigeons have to share (here map on to) the same hole.

QED.

We now prove the following claim over finite sets .

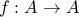Claim Let be a finite set. Prove that every one-to-one function f: A rightarrow A is also onto.

Proof

We will prove by contradiction.

Let 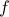be a one-to-one function as above but not onto.
Therefore, 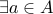such that for every , .
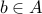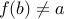Therefore, 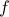can be written as a one-to-one function from 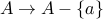(since nothing maps on to ).
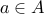Similarly, we repeat this process to remove all elements from the co-domain that are not mapped to by 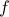to obtain a new co-domain .
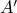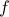is now a one-to-one and onto function from to .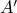
However, 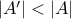. Therefore by pigeon-hole principle 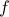cannot be one-to-one.

The last statement directly contradicts our assumption that 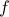is one-to-one. QED.

Infinite Sets

We now note that the claim above breaks down for infinite sets.

Let us take 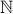mathbb{N} , the set of all natural numbers.

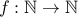defined by 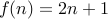is one-to-one.
However, 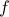is not onto.

Hilbert's Hotel

Consider a hotel with infinitely many rooms and all rooms are full.

An important guest arrives at the hotel and needs a place to stay. How does the manager accommodate the new guests even if all rooms are full?
Each one of the infinitely many guests invites his/her friend to come and stay, leading to infinitely many more guests. How does the manager accommodate these infinitely many guests?

One-to-One Correspondences of Infinite Set

There is a one to one correspondence between the set of all natural numbers 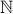mathbb{N} and the set of all odd numbers .

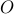Take 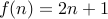f(n) = 2 n +1 , where 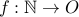f: mathbb{N} rightarrow O . We note that 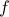is a one-to-one function and is onto.

Can we say that 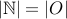|mathbb{N}| = |O| ? Yes, in a sense they are both infinite!! So we can say 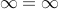infty = infty !! Therefore we conclude that

There are “as many” even numbers as there are odd numbers?
There are “as many” positive integers as there are integers? (How can a set have the same cardinality as a subset of itself? :-)
There are “as many” prime numbers as there are natural numbers?

Note that “as many” is in quotes since these sets are infinite sets.

Infinite Sets

There are many ways to talk about infinite sets. We will use the following “definition”:

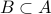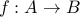A set is infinite if and only if there is a proper subset B subset A and a one-to-one onto (correspondence) f: A rightarrow B .

Here are some examples of infinite sets:

Natural numbers 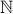: The odd numbers 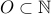. We just proved a one-to-one correspondence between natural numbers and odd numbers.
Integers 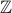are an infinite set. The correspondence .
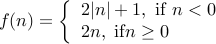Rational numbers 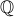: We will prove a one-to-one correspondence between rationals and integers 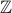next class.