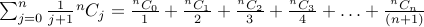Lecture 24: Combinations
Take a set  with
with  elements:
elements:  .
A
.
A  combination from
combination from  is a subset
is a subset  formed by choosing any
formed by choosing any  elements from
elements from  :
:
Each element can be chosen at most once.
The order does not matter.
The number of 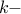 combinations of
combinations of  elements is written
elements is written 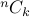 .
.
Example-1
There are 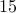 players available to our coach of which she can choose to form a team consisting of
players available to our coach of which she can choose to form a team consisting of 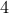 people.
How many possible choices of teams does she have?
people.
How many possible choices of teams does she have?
Answer We have a set of size 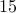 people. What is needed here is a
people. What is needed here is a 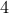 -combination from this set.
The answer is therefore
-combination from this set.
The answer is therefore 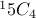 .
.
Example-2
There are  teams in a round-robin tournament where each pair of teams play exactly one match. How many matches need to be played?
teams in a round-robin tournament where each pair of teams play exactly one match. How many matches need to be played?
Answer Each match is a 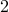 -combination from the set of
-combination from the set of  teams. Therefore, the number of matches is
teams. Therefore, the number of matches is 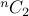 .
.
Example-3
A cricket coach can make up a team of  cricketers amongst
cricketers amongst 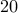 possible candidates. She has
possible candidates. She has
Plans to have
 specialist bowlers (pitchers) have
specialist bowlers (pitchers) have 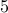 to choose from.
to choose from.Plans to have
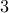 specialist batsmen (hitters) and have
specialist batsmen (hitters) and have 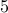 to choose from.
to choose from.Plans to have
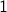 wicketkeeper and has
wicketkeeper and has 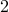 to choose from.
to choose from.Plans to have
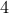 all-rounders (pinch hitters+relief pitchers) and has
all-rounders (pinch hitters+relief pitchers) and has 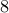 to choose from.
to choose from.
How many possible choices of teams does she have, given her plans above.
Answer 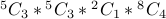 .
.
Example-4
There are 10 stalls in the farmer's market. Each stall sells apples and oranges. We can (a) skip a stall, (b) buy two apples in each stall or (c) alternatively buy two oranges.
How many ways are there of buying 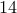 apples and
apples and 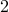 oranges.
oranges.
Computing the Number of Combinations
So far, we have seen 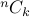 . What exactly is it in terms of numbers? There are two ways of thinking about it:
. What exactly is it in terms of numbers? There are two ways of thinking about it:
From Permutations to Combinations
In a  -permutation of
-permutation of  elements:
elements:
We choose
 out of
out of  .
.All choices need to be distinct.
Finally, order of choice matters.
The number of  -permutations is
-permutations is 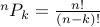 .
.
In a  -combination, the order of choice does not matter.
-combination, the order of choice does not matter.
Let us relate  -permutations and
-permutations and  -combinations.
-combinations.
Here is a way of looking at  -permutations:
-permutations:
Choose a
 -combination from the set (
-combination from the set (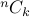 possible choices)
possible choices)Choose an order of the chosen elements (
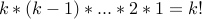 possible choices).
possible choices).
Thinking about things above, we get the following identity: 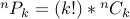 .
.
We already reasoned out 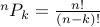 . Therefore, the formula for
. Therefore, the formula for 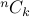 should be
should be
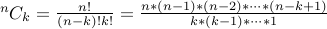
Let us play around with it:
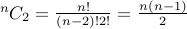
What are expressions for
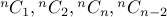 and so on?
and so on?What is
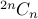 ?
?
Claim 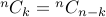 .
.
Let us give an intuitive reason for this: 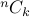 means choosing
means choosing  elements out of a total of
elements out of a total of  . We can look at it also as choosing which elements to include or choosing which elements to exclude.
There are
. We can look at it also as choosing which elements to include or choosing which elements to exclude.
There are 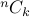 ways of choosing elements to include in our subset. On the other hand, there are
ways of choosing elements to include in our subset. On the other hand, there are 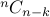 ways of choosing which elements to exclude. Both views are counting the same
thing. Therefore they better be the same.
ways of choosing which elements to exclude. Both views are counting the same
thing. Therefore they better be the same.
Mathematically, just write down the formulae:
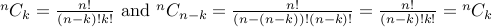
Example-1
Six people would like to sit around a round table. It does not matter where a person sits, but what matters is who sits next to him/her. In other words, choices 1,2,3,4,5,6 or 6,1,2,3,4,5 are the same since each choice leaves the same neighbors. How many possible seating choices are there?
Answer Let us say the number is 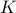 . We see that once we choose a seating order, we can obtain
. We see that once we choose a seating order, we can obtain 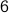 different permutations of it that are equivalent since they correspond to the
same seating order. Therefore
different permutations of it that are equivalent since they correspond to the
same seating order. Therefore 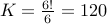 .
.
Recursively Counting Combinations
Here is another way of thinking. We need to choose a subset of  elements from a set of size
elements from a set of size  :
: 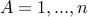 .
.
-
If
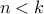 then we have no choice. If
then we have no choice. If 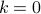 then we have
then we have 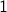 choice (the empty set) and if
choice (the empty set) and if 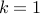 then we have
then we have  choices.
choices. Otherwise, choose whether or not to include the smallest numbered element
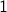 .
.
If we decide to select
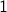 , we have to choose
, we have to choose 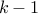 from the remaining
from the remaining 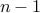 .
. If not, we have to choose
 from the remaining
from the remaining  .
.
Therefore
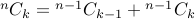
Connection between 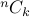 and the Pascal's triangle in class.
and the Pascal's triangle in class.
Binomial Theorem
Now for a bit of algebra. Let us consider polynomials 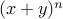 .
.
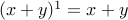 .
.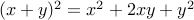 .
.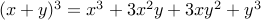 .
.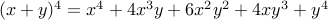 .
.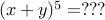 (answer in class).
(answer in class).
The question is what 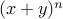 should be.
should be.
Take 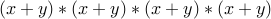 . I am interested in the coefficients of various terms.
. I am interested in the coefficients of various terms.
Let us start with 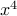 .
.
Why is its coefficient
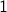 ? If we look at it there is just one way to form
? If we look at it there is just one way to form 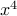 (by choosing
(by choosing 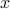 from all the
from all the 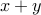 ).
).On the other hand, why is the coefficient of
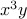 equal to
equal to 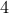 ? The answer is that there are
? The answer is that there are 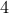 possible ways in which
possible ways in which 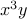 is formed in the product. Can you identify them?
is formed in the product. Can you identify them?
How many ways are there of forming 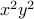 ? Simple, we have to choose 2
? Simple, we have to choose 2 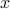 s (the remaining
s (the remaining 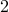 will naturally yield
will naturally yield 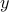 ). There are four possible multiplicands
). There are four possible multiplicands 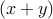 of which
we can choose
of which
we can choose 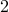 “x” in
“x” in 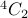 ways.
ways.
If you understood the argument above then you have understood the theorem we are about to prove.
Binomial Theorem
For all natural numbers  , we can expand
, we can expand
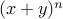 as
as
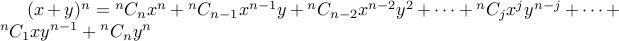
We can write it succinctly as 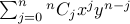 .
.
Proof What is the coefficient of 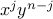 in
in 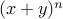 .
We write
.
We write 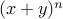 as
as 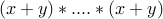 .
There are
.
There are  multiplicands.
multiplicands.
To form a term 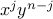 where
where 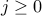 , we can choose
, we can choose 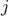 out of
out of  multiplicands to “supply” the
multiplicands to “supply” the 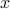 . The remaining will be chosen automatically to supply the
. The remaining will be chosen automatically to supply the 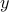 s.
There are
s.
There are 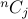 choices. Each choice appears as a term which are then collected up.
choices. Each choice appears as a term which are then collected up.
Our reasoning above shows that the coefficient of 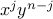 where
where 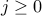 should be
should be 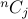 .
.
Example-1
Expand 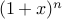 ?
?
Answer 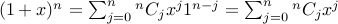 .
.
Applications of Binomial Theorem
We can use the Binomial theorem to show some properties of the 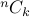 function.
function.
1. 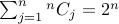 .
.
Proof: Take the expansion of 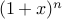 and substitute
and substitute 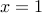 .
.
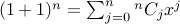
2. Let  be an even number. Then we have
be an even number. Then we have 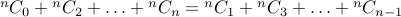 .
.
Proof: Take 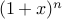 and set
and set 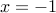 . Write a similar result for
. Write a similar result for  odd.
odd.
3. Evaluate: 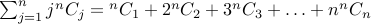 .
.
Proof: Take 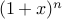 . Using binomial theorem, we have
. Using binomial theorem, we have
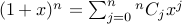 .
.
Take the derivative of both sides w.r.t 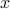 . We get:
. We get:
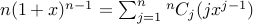
Substituting 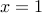 , we get the required summation to be
, we get the required summation to be 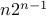 .
.
4. Likewise, can you evaluate this summation: