
Currently, the rate at which simulation data can be generated far outstrips the rate at which scientists can inspect and analyze it. 3D visualization techniques provide a partial solution to this problem, allowing an expert to scan large data sets, identifying and classifying important features and zeroing in on areas that require a closer look. Proficiency in this type of analysis, however, requires significant training in a variety of disciplines. An expert analyst must be familiar with domain science, numerical simulation, visualization methods, data formats, and the details of how to move data across heterogeneous computation and memory networks, among other things. At the same time, the sheer volume of these data sets makes this task not only arduous, but also highly repetitive. One logical next step is to automate the feature recognition and characterization process so scientists can spend their time analyzing the science behind promising or unusual regions in their data, rather than wading through the mechanistic details of the data analysis. The goal of this project was to develop a tool that does so.
General definitions of features are remarkably hard to phrase; most of those in the literature fall back upon ill-defined words like ``unusual'' or ``interesting'' or ``coherent.'' Features are often far easier to recognize than to describe, and they are also highly domain-dependent. The structures on which an expert analyst chooses to focus --- as well as the manner in which he or she reasons about them --- necessarily depend upon the physics that is involved, as well as upon the nature of the investigation. Meteorologists and oceanographers are interested in storms and gyres, while astrophysicists search for galaxies and pulsars, and molecular biologists classify parts of molecules as alpha-helices and beta-sheets. Data types vary --- pressure, temperature, velocity, vorticity, etc. --- and a critical part of the analyst's expert knowledge is knowing how different features manifest in different data fields.
Our goal was to create a general-purpose feature
characterization system and to validate it with a variety of specific
instances of problems in different fields. As a first step, we focus
on finite element analysis data from computer simulations of solid
mechanics problems. Since we want to produce a practical, useful
tool, we are working with data from deployed simulators, in a
real-world format: ASCI's DMF (Data Models & Formats), a lingua
franca used by several of the US national labs to read and write
data files for large simulation projects. This choice raised some
interesting interoperability issues that are described in the papers
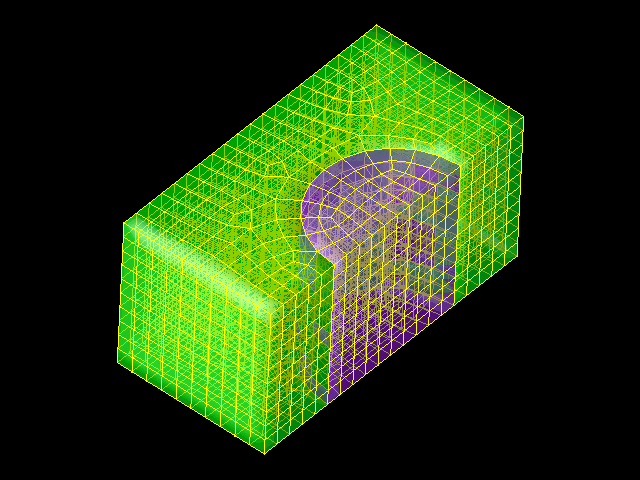
cited below. A DMF data snapshot consists of a geometric description
of a mesh (generally 2D or 3D) and some information about the physics
at each mesh point. Here is an example of such a snapshot-- a simple
meshed surface in 3D:

Given such a snapshot, our goal is to characterize the features
therein and generate a meaningful report. In this case, the surface
is basically smooth with the exception of a single "spike." Spikes
are interesting for both numerical and physical reasons, and our
algorithms use patterns in the normals to adjacent mesh elements in
order to find them. The image below shows the same surface, but with
each mesh element rendered in a color that indicates how much its
normal vector deviates from the average of the normal vectors of its
neighbors:
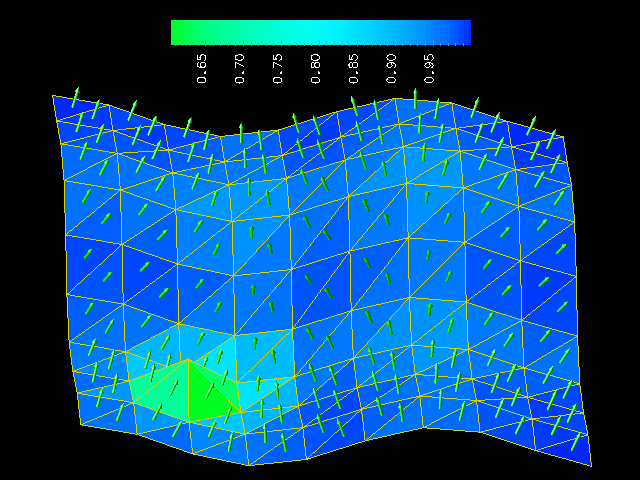
In order to understand what makes a feature, we began by working closely with domain scientists to identify a simple ontology of distinctive coherent structures that help them understand and evaluate the dynamics of the problem at hand. (Formally, an ontology seeks to distill the most basic concepts of a system down into a set of well defined nouns and verbs -- objects and operators -- that support effective reasoning about the system.) In finite-element applications, as in many others, there are two kinds of features that are of particular interest to us:
