NOTE: If the mathematical symbols on this page are not rendered correctly, please go here for instructions on adjusting your browser settings.
Our paper demonstrates that such attacks are pervasive when the integrity of ciphertexts is not guaranteed. We first review Vaudenday's attack and give a slightly more efficient version of it. We then generalize the attack in several directions, considering various padding schemes, other symmetric encryption schemes, and other side-channels, demonstrating attacks of various strengths against each. Finally we argue that the best way to prevent all of these attacks is to insist on integrity of ciphertexts [BN00] in addition to semantic security as the ``proper'' notion of privacy for symmetric encryption schemes.
Following the chosen-ciphertext attack of Bleichenbacher, RSA PKCS #1 v.1 was abandoned in favor of a scheme with chosen-ciphertext security (CCA) [Ble98,Pub98]. It is now expected that any new public-key cryptosystems will provide CCA security. However most symmetric encryption schemes attain, at best, semantic security against chosen plaintext attacks [BDJR97].
Vaudenay recently demonstrated a side-channel attack against CBC Mode encryption with CBC-PAD [Vau02,BR96]. Given an oracle which reveals whether or not the plaintext (corresponding to some altered ciphertext) is correctly padded, he showed that one can efficiently recover the plaintext.
A reasonable reaction to this attack is to seek other padding methods or other encryption schemes which do not succumb to this particular attack. However, as we show, this type of weakness is pervasive: it occurs for many natural padding schemes, and in most common encryption schemes. Vaudenay's paper focuses on the CBC-PAD padding method and comments on a few others. In this paper we examine several classes of padding schemes and show it is actually quite rare for CBC to retain semantic security in the presence of a ``valid padding'' oracle when using any of these schemes, including the commonly-used 10* padding where one pads by appending a single 1 bit and then zero or more 0 bits. We also show that all other commonly-used symmetric encryption schemes are similarly vulnerable in the prescence of a ``valid padding'' oracle.
It is most-likely possible to get around these weaknesses by ridding ourselves of the oracle in one way or another. However one can easily imagine other oracles which might arise in practice which would provide similar powers to the adversary if he retains the ability to to freely induce predictable changes in the plaintext via modification of the ciphertext. For example, imagine a cryptographic relay which accepts ciphertext encrypted by one scheme and outputs ciphertext under another [JDK+91]. If the first scheme uses some padding method and the second is length-revealing, we effectively have an oracle which divulges the length of the padding used by the first scheme. There are doubtless other examples as well. Therefore our view is this: these weaknesses are not faults of padding schemes or relays or anything of this nature; they follow directly from the fact that an adversary can reliably and efficiently produce valid ciphertexts which have a predictable relationship with the underlying plaintext, even if he knows virtually nothing about the plaintext.
Several schemes have been proposed to provide authenticity of ciphertexts at a very low cost [BN00,Jut01,RBBK01]. Our hope is that, similar to the public-key domain, researchers and practitioners will insist on this stronger notion of security for symmetric encryption to obviate the simple weaknesses listed above.
CONTRIBUTIONS. This paper makes a number of observations concerning the power of possessing a valid-padding oracle. Our starting point is the attack on CBC Mode encryption with CBC-PAD from [Vau02]. We begin by reviewing this attack. Then
Finally, we argue that such side-channels are bound to crop up again and again as long as we allow the adversary to freely manipulate ciphertexts, and we argue in favor of adopting the combination of chosen-plaintext security and integrity of ciphertexts [BN00] as the standard requirement for symmetric encryption schemes, even when privacy is the only goal.
RELATED WORK. CBC Mode encryption has the property that flipping a particular bit in the i-th block of ciphertext will flip the same bit in the i+1-st block of underlying plaintext. The fact that this property can be exploited by attackers has been known for some time. Bellovin published an attack on CBC where the IV was altered to effect a change in the first block of the received plaintext [Bel96]. Also in [Bel96], an attack (very similar to the attacks in this paper) is described which recovers plaintext bits by sending altered ciphertexts to a TCP peer which then acts as a validity oracle for each packet by either dropping it or returning an ACK for it. A cleaner example of this attack is described in an attack on WEP by Borisov, Goldberg, and Wagner [BGW01].
Bleichenbacher demonstrated that side-channels in the asymmetric setting could be used to mount a chosen-ciphertext attack against RSA PKCS #1 v.1 [Ble98]. Bleichenbacher's side-channel was a ``valid formatting'' oracle similar in spirit to the ``valid padding'' oracle used by Vaudenay. Manger followed this by showing how RSA PKCS #1 v.2, a scheme with chosen-ciphertext security (in the random oracle model), could be similarly exploited assuming a different side-channel [Man01]. Manger's side-channel requires an oracle indicating that an error occurred between the decryption and integrity-check phases of the algorithm. In a more theoretical setting, Krawczyk showed how a stream encryption mode (under an unusual plaintext encoding) combined with a MAC would yield a side-channel attack based on message validity if the order was encode, then authenticate, then encrypt [Kra01]. His goal was to show that this ordering of primitives was not generically secure. Vaudenay was the first to show that message padding might create similar side-channels under CBC Mode encryption [Vau02]. His attack requires an oracle indicating whether or not the padding of an underlying plaintext is valid.
NOTATION. For any nonnegative integer n, let {0,1}n represent the set of bit strings of length n. Let e represent the empty string. For two strings A and B we write A || B or simply AB to denote their concatenation. For the XOR of A and B we write A Å B. Let ||A|| denote the length of A in bytes, and |A| the length of A in bits. We write A[i] to mean the i-th bit of A, counting from zero, starting from the leftmost bit of A. We write A[i¼j] to mean the substring of A starting at position i and ending at position j.
In general, if S is a set we write S+ to mean 1 or more repetitions of elements from S; that is, the set {s1 s2 ¼sm | m > 0, si Î S, 1 £ i £ m}.
A function family from n-bits to n-bits is a map E:K×{0,1}n® {0,1}n where K is a finite set of strings, typically the set of strings all of some fixed length. It is a block cipher if each EK(·) = E(K,·) is a permutation. We can build an encryption scheme from a block cipher using any of various standard modes of operation.
CBC MODE ENCRYPTION. Given a block cipher E : {0,1}k ×{0,1}n ® {0,1}n, a k-bit block-cipher key K, and some message M Î ({0,1}n)+, we write M as the concatenation of l strings each n-bits long, M=M1 M2 ¼Ml. To encrypt M under key K, we randomly select an n-bit value, the IV, and set C0 ¬ IV. We then compute Ci ¬ EK(Mi Å Ci-1) for each 1 £ i £ l. The ciphertext is (IV, C1 C2 ¼Cl). In the standard model, CBC is provably-secure against chosen-plaintext attack with good bounds: assuming the underlying block cipher is ``good,'' an adversary has little chance to distinguish the CBC Mode encryption of a given plaintext from the CBC Mode encryption of random bits. (For a precise definition and proof, see [BDJR97].)
PADDING. The above description assumes that the length of M is a multiple of the block size n. In practice this may not be the case, and therefore it is common to apply a padding function PAD: {0,1}* ® ({0,1}n)+ to M. We say a padding function is reversible if the function is injective; in other words, reversible means one can always uniquely recover M given PAD(M). Most applications require the padding function to be reversible. Often the padding function brings |M| up to the next multiple of n, but nothing precludes expanding M even further; indeed, SSL will sometimes add several blocks of padding when using CBC-PAD.
We consider two classes of padding: byte-oriented padding and bit-oriented padding. Byte-oriented padding functions assume that both n and |M| are multiples of 8. Bytes are then appended to the end of M in some well-defined manner to bring its length up to a multiple of n. Bit-oriented padding functions take a message M of any bit-length and append bits to M to bring |M| up to a multiple of n.
We now sketch Vaudenay's attack from [Vau02] which will serve as a warm-up for later discussion. We also show an improvement which deterministically finds the length of the padding in lg(b) oracle queries, where b is the number of bytes per block.

CBC-PAD. The well-known CBC-PAD function [BR96] is byte-oriented: CBCPAD: ({0,1}8)+ ® ({0,1}n)+. Assume |M| is a multiple of 8, and let n=8b (for virtually all real block ciphers, b is at most 32). Let p = ||M|| mod b, so p is the number of bytes we must pad (assuming we wish to add the least possible amount of padding). If p=0, we set p=b. Finally, we write p as a byte and append it p times to the end of M. So if there is one byte left to pad, we append a single 01 to M; if there are two bytes of pad needed we append 02 02 to M, and so forth. Clearly this method is reversible: given CBCPAD(M) we can uniquely recover M.
Although CBCPAD(·) is reversible, it is not bijective: what should the receiver do after decryption if he finds that the recovered plaintext is not in the function's range? That is, what is the proper action if the padding is invalid? This of course depends on an implementation detail. Some protocols specify that the session be torn down (SSL/TLS), others just log the error (ESP [KA98]), and others return an error message (WTLS [Wir01]). Vaudenay recently made the observation that if one can ascertain somehow the padding error status, it can be used as a side-channel to mount a chosen-ciphertext attack in the symmetric-key setting [Vau02]. He showed how, given an oracle O which accepts a ciphertext and returns either VALID or INVALID depending on whether the corresponding plaintext is properly padded, one can recover the underlying plaintext. His attack requires a single ciphertext, and a number of oracle queries proportional to the number of bytes in the padded message.
THE ATTACK. Let's say we have an oracle O as described above: O accepts ciphertexts, decrypts using CBC under the secret key K, and recovers the corresponding plaintext M¢. If M¢ is correctly padded (ie, M¢ = CBCPAD(M) for some M), then O returns VALID. Otherwise O returns INVALID. We now mount a chosen-ciphertext attack on CBC Mode encryption. (A point of clarification: normally a ``chosen-ciphertext attack'' implies that we have access to a decryption oracle which supplies the plaintexts for ciphertexts of our choice. Here we have something different: an oracle which does accept ciphertexts but returns only a bit. It is important to keep this distinction in mind.)
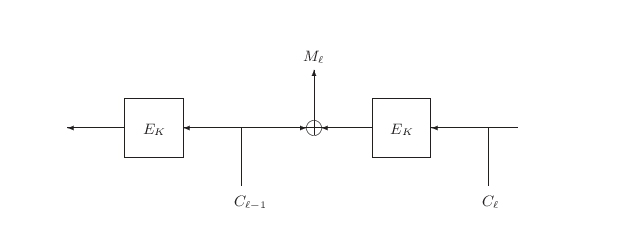
The attack works as follows: we obtain some ciphertext C under the secret key K. For simplicity, suppose C is two blocks (IV, C1). (The attack generalizes easily to longer ciphertexts.) As shown in Figure 1, the oracle will compute the CBC Mode decryption of C in the standard way, and any changes to IV will cause changes to the plaintext block M1. Initially, M1 is a correctly-padded block of plaintext. However, by manipulating the bits of IV we can cause predictable changes within M1 and infer a great deal about its contents.
Vaudenay's attack works in two phases. First he randomly flips bits in IV until O(C) = VALID. Once this occurs, we know we must have induced an M¢1 with a proper CBC-PAD. That is, our induced M¢1 must end in 01, or 02 02, or 03 03 03, etc. The probability that each occurs is 1/28, or 1/216, or 1/224, etc., respectively. The event O(C) = VALID should therefore occur in at most 128 expected queries, and once it does it is highly-likely that we induced a 01 in the final byte of M¢1. (The less-probable cases can be detected with a few additional oracle queries.) And once we know the value of the final byte in the induced M¢1, we know the value of the final byte in M1: say IV¢ is the IV which induced a 01 in the final byte of M¢1. Then the final byte of M1 is simply the final byte of IV¢ Å 01.
Vaudenay then iterates the method using the above technique as a subroutine. He therefore decrypts a block in about 128b expected oracle queries (recall b is the number of bytes per block).
AN IMPROVEMENT. While our main aim in this paper is to show how widely we can generalize the above ideas, we first note a simple improvement to the attack above which greatly improves its efficiency for short messages.
Suppose we again have a padding oracle O and a ciphertext C=(IV, C1). We know that M1 has a valid CBC-PAD as before. We mount a binary search to discover which of the b possible pad-values was used, as follows: first, notice that inducing a change in any padding byte (except the final byte) of M1 will always cause O to return INVALID. Also notice that inducing a change in any message byte (ie, a non-padding byte) of M1 always causes O to return VALID. We may therefore perform a binary search by altering a single byte at a time. Number the bytes of IV starting from the right end, beginning from 1. That is, write IV = ib ib-1 ¼i2 i1, where each ij is a byte. Let IVm be equal to IV but with its m-th byte complemented (complementation is an arbitrary choice; any change to the m-th byte will do). That is, IVm = ib ¼im+1[`(im)] im-1 ¼i1, where [`(im)] denotes bit complementation. We use values of m from b down to 2 to find the length of the padding in M1. Variables IV, C1, and O are assumed to be global, and the algorithm is initially invoked with FIND-LEN(b,1).
FIND-LEN(i,j)
if i=j then return i
m ¬ é[(i+j)/2] ù
if O(IVm, C1) = INVALID then
FIND-LEN(i, m)
else
FIND-LEN(m-1, j)
The algorithm finds the length of the padding in lg(b) steps where b is the length of a block in bytes and lg() is log2(). So our improved algorithm first finds the length of the padding as above, then uses Vaudenay's method on the remainder of the block. If we assume the length of the padding is uniformly distributed between 1 and b, this new algorithm finds the plaintext associated to a padded block in an expected 64b + lg(b) oracle queries. This is a substantial improvement for short messages only.
While CBC-PAD is certainly a common byte-oriented method, there are several other schemes in common use, and some natural ones not in use. We now survey the most natural schemes and classify their vulnerabilities to this type of attack. The purpose here is to demonstrate that virtually all common padding schemes are vulnerable to some kind of attack based on ``valid padding'' side-channels under unauthenticated CBC Mode encryption. Our results are summarized in Figure 2.
For each scheme listed here, we focus on attacking single block messages where the ciphertext looks like (IV, C1). This generalizes easily to multi-block messages since we can attack each block individually by using the prior block of ciphertext as an IV. That is, given ciphertext (IV, C1, C2, ¼), we attack block Cj by attacking the two-block ciphertext (Cj-1, Cj) where here Cj-1 is acting as the IV.
| Bit- | Byte- | Loss of | # Queries to Find | Exp # Queries to | |
| Scheme | Oriented | Oriented | Semantic Security? | Padding Length | Recover Plaintext |
| CBC-PAD | × | Y | lg(b) | 64b + lg(b) | |
| ESP-PAD | × | Y | lg(b) | 64b + lg(b) | |
| XY-PAD | × | Y | lg(b) | 64b + lg(b) | |
| OZ-PAD | × | Y | n/a | 28b-1 | |
| BOZ-PAD | × | Y | lg(b) | 64b + lg(b) | |
| PAIR-PAD | × | Y | n/a | 28b-8 | |
| ABYT-PAD | × | N | n/a | n/a | |
| ABIT-PAD | × | N | n/a | n/a |
ESP PADDING (ESP-PAD).
The padding scheme for IPSec's Encapsulated Security Payload is
similar to the CBC-PAD method we saw above. It is a reversible
byte-oriented padding scheme; if we have to pad p > 0 bytes, we append
the bytes 01 02 ... up to p.
As mentioned in [Vau02],
a valid-padding oracle for this method also allows recovery of the
plaintext; our improvement from Section 3 works here as well.
XY PADDING (XY-PAD). This byte-oriented method uses two distinct public constant byte-values X and Y. We transform M by first appending X one time (mandatory), then adding the necessary number of Y values. Clearly this method is reversible: M is easily recovered after padding by removing all trailing Y bytes and the last trailing X byte. And once again, this method succumbs to the attacks described above, including our improvement from Section 3, although in this case we must take care to avoid converting X to Y when we perform the IV alteration; since we are not constrained in how we make this alteration, and since we know the public values X and Y, we can simply avoid this problem.
OBLIGATORY 10* PADDING (OZ-PAD). The so-called ``obligatory 10* padding'' is a bit-oriented padding scheme; it works as follows: append a 1-bit to M (mandatory) and then zero or more 0-bits as necessary to fill out the block. This is the bit-oriented version of the XY padding method above, and is similarly reversible: remove all trailing 0-bits and the last 1-bit.
But suddenly it seems the attacks we discussed above no longer apply. The key difference is this: virtually every plaintext string is a correctly-padded string since the only requirement for validity is that there is a 1-bit somewhere.
This is encouraging in some sense: many standards recommend obligatory 10* padding and therefore seem more robust against these side-channel attacks. However, there is one plaintext block which is invalid under this padding definition: 0n. Suppose O were an oracle which accepts CBC-encrypted ciphertext and returns VALID whenever the final block of the corresponding plaintext contained at least one 1-bit, and INVALID when it was all zeroes. It's clear that this, once again, enables one to entirely recover the plaintext, but there is no efficient method for recovering the plaintext. The problem is this: in order to get the oracle to report INVALID we must essentially ask O(IV¢, C1) where IV¢ = IV Å M1. In other words, we must guess what M1 is in order to get a response of INVALID. Therefore, our oracle is simply answering ``yes'' or ``no'' to our guesses about what the plaintext block is. If we assume the plaintext is uniform and random, it will take an expected 28b-1 guesses to guess correctly.
However, this is not to say that such an oracle is useless. In fact, in the presence of such an oracle, CBC Mode encryption does not retain semantic security. One incarnation of semantic security plays the following game: we submit a value to an oracle and it encrypts either the value we submitted or some random value. If we can guess which choice it made with probability much larger than 1/2, we win. Clearly in the presence of our valid-padding oracle we can win this game for CBC encryption with probability essentially 1. We merely ask the encryption oracle to encrypt some random block M1, it returns ciphertext (IV, C1), then if O(IV Å M1, C1) = INVALID we know M1 was (with overwhelming probability) the value encrypted.
But what does this mean in practice? Well, if we have a set of candidate blocks which we suspect might match the plaintext for a given ciphertext block, the valid-padding oracle will allow us to determine which of them, if any, is the correct one. This is perhaps not as far-fetched as it sounds: natural-language plaintexts commonly contain salutations, addresses, and other standard sections in their bodies. Structured documents will often contain headers with a well-known format. It should be desirable to hide all of this information!
As a final comment: one could eliminate this problem by simply defining the block 0n to be a valid block of plaintext and (say) removing it. But we must then also be careful to define what happens to the preceding block (if any). Do we also remove padding bits from it or do we stop? One virtue of 10* padding is that it is simple; adding complexity to its definition merely increases the chance that we will implement O via implementation errors.
A BYTE-ORIENTED VERSION OF 10* PADDING (BOZ-PAD). It might be tempting to implement 10* padding in a byte-oriented manner by appending 0x80 once and then as many 00 bytes as needed to fill out the block. This is probably how most applications generate padding when they know the plaintext will already be byte-aligned and need to use 10* padding. If, however, the receiver depends on this, and that dependence is externally manifested, we once again have a useful valid-padding oracle. In other words, if the receiver somehow indicates whether or not the padding is 80h followed by zero or more 00 bytes, we have a specific instance of the XY Padding method mentioned above.
ARBITRARY-PAIR PADDING (PAIR-PAD). An interesting try at avoiding the weaknesses involved with XY Padding is to allow any distinct values X and Y. The sender is still free to use whatever values he wishes, and they need not be random provided they are not fixed public constants. Once the sender decides on the X and Y values, he pads by appending X once and Y one or more times to bring the message up to the desired length. (Here we must require Y be appended at least once else the padding method is not reversible.) This padding method is identical to XY-PAD; the difference is in how the padding is removed. The receiver allows any two distinct values, so the algorithm to remove the padding is to first remove all matching trailing byte values at the end of the string, and then also remove the byte preceding these matching values. This nearly removes the oracle since, like 10* padding, nearly all plaintext blocks are correctly padded. However, again like 10* padding, there remains the case where all bytes are equal in a block. If we have an oracle telling us when all bytes are equal, we can again mount an attack similar to the one described for 10* padding. But random guessing will not be efficient here since, assuming random and uniform plaintexts, it would take an expected 28b-8 queries just to get an INVALID response from the oracle. (Although we cannot tell which byte is repeated in the plaintext when we get an INVALID from the oracle, we know there are only 256 possibilities left for the plaintext and-assuming it has some structure-we should be able to recover the plaintext at this point.)
ARBITRARY-TAIL PADDING (ABYT-PAD). A better byte-oriented padding method is this: the sender examines the last byte X of the message M. He picks an arbitrary distinct byte-value Y and uses Y to pad (if M is the empty string, he picks any byte-value for Y.) He then pads M with Y, adding one or more bytes of Y to the end of M as desired (note that he must add at least one!).
The receiver merely removes all matching trailing bytes until either a distinct byte is found (which is left intact) or the empty string is reached. This method is clearly reversible, and all plaintexts are valid so there is no attack of the type mentioned in this paper. The oracle has been removed entirely.
Notice that the sender need not generate random values here: he may instead follow a well-defined rule such as
As before, the receiver cannot depend on any such rule, since otherwise we may once again implement some oracle suitable for use in an attack.
A BIT-ORIENTED ANALOG (ABIT-PAD). There is an obvious bit-oriented analog here as well: the sender examines the last bit of M and pads with repetitions of the opposite bit, always adding at least one bit of padding. For M = e he pads with 0-bits. Once again, all plaintexts are valid and the oracle is removed.
PADDING THE CIPHERTEXT. Another simple approach to removing the oracle is to use some length-preserving variant of CBC Mode. There are several ways of doing this, with ``ciphertext stealing'' probably the most well-known [BR96]. Since there is no padding, there is no padding oracle, and the above attacks vanish. If there is still a need to pad (because, for example, we require the ciphertext end on an alignment boundary), we could then pad the ciphertext.
One problem with this approach is that the length of the plaintext is divulged to a bit granularity and this may be undesirable. (See the next section for further discussion.)
Thus far we have focussed exclusively on CBC Mode encryption. While CBC Mode encryption is certainly ubiquitous, it is by no means the only symmetric encryption scheme used. In fact, the RC4 stream cipher is often the encryption method of choice for SSL/TLS. Other block-cipher modes generate streams used as one-time pads as well: Output-Feedback Mode (OFB), Cipher-Feedback Mode (CFB), and Counter Mode (CTR) all fall into this class [MvV96]. It is therefore natural to ask if the padding attacks mounted against CBC apply to these schemes as well. The answer is: maybe.
The reason we say ``maybe'' is because padding may or may not be used with stream-based encryption schemes. When encrypting with a pseudorandom bit-stream, we are free to use exactly the number of bits needed; there is no need to pad. However in practice we find it is quite common to add padding even when using stream-based schemes. The motivation is this: when performing encryption we are normally willing to divulge two things: (1) communication is taking place, and (2) the length of this communication.
But for short strings we may wish to slightly obscure the length of the communication. As an extreme example, if we are encrypting a single bit, an adversary quickly knows the plaintext is one of only two values. Padding serves as a way to at least partially obscure the length of the plaintext.
If padding is used, the potential for a valid-padding side-channel resurfaces. This arises because stream-based encryption is simply the XOR of the plaintext with a pseudorandom bit-stream (Figure 3). Therefore, as with CBC Mode, we may flip plaintext bits merely by flipping the corresponding ciphertext bits. The only difference here is that in CBC Mode we flipped bits in Cl-1 to affect bits in Ml, and here we flip bits in Cl instead.
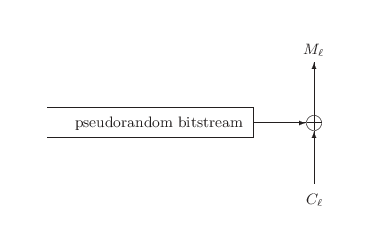
Therefore we see our current collection of attacks is not restricted solely to CBC Mode encryption but will occur with several common schemes if the plaintext is padded. In [Vau02] we find further examples of modes (all CBC variants) which succumb to padding attacks. The lesson here is that none of these modes is trying to prevent an adversary from manipulating the ciphertext, and the fact there exist attacks against a wide variety of padding schemes and encryption schemes based on manipulation of the ciphertext should be no great surprise.
All prior attacks considered how to exploit a valid-padding oracle to recover the underlying plaintext for any given ciphertext, assuming the use of a variety of padding methods. But given the power to freely and predictably alter the underlying plaintext via manipulations of the ciphertext, one might expect that a variety of other oracles would be equally useful to an attacker. In this section we describe an oracle which divulges the bit-length of an underlying plaintext and we show that such an oracle would also result in highly-efficient attacks.
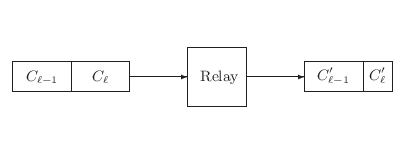
A LENGTH-REVEALING ORACLE. A cryptographic relay is a device which accepts ciphertext under one scheme and outputs ciphertext under another (usually with a different key). Probably the most natural setup is where the incoming and outgoing schemes are the same, but it is certainly conceivable that they might be different. Routers which handle a variety of physical-layer network protocols are common, so a secure router might handle a variety of cryptographic protocols.
Imagine a relay where the incoming scheme pads the plaintext to a block boundary but the outgoing scheme uses some length-preserving mode (Figure 4). If an adversary can view the ciphertext on both sides of the relay, he effectively has an oracle which divulges the length, within a block, of the underlying plaintext. In the presence of this oracle, even those padding schemes which resisted valid-padding oracle attacks now succumb.
Consider the following example: suppose the incoming ciphertext block Cl is produced by encrypting plaintext which is padded with 10* padding, but the outgoing ciphertext uses some length-preserving scheme such as CTR Mode. Then we can mount an attack, regardless of the encryption scheme used, more efficient than any we have seen thus far. Using our oracle we know the exact position of the last trailing 1-bit in the underlying ciphertext. Suppose it is in bit-position i of a plaintext block Ml, counting bits from 1 starting on the left end. We then flip bit i by manipulating the ciphertext appropriately, and submit this to the oracle which divulges the position of the new rightmost 1-bit. In this manner, we collect up the positions of all the 1-bits in w(Ml) oracle queries, where w() denotes the Hamming weight of Ml.
And even our ``perfect'' Arbitrary-Tail Padding methods from Section 4 (ABYT-PAD, ABIT-PAD) fail in the presence of this oracle, which now leads us to look for new methods which remain secure in this new setting. And so on.
It is likely that many innocent-looking oracles could give rise to attacks in the style above, and it is probably difficult to avoid implementing such oracles in real systems. However, each attack we examined depended on the adversary's ability to freely and predictably alter bits of the plaintext via manipulation of the ciphertext, and this ability was granted by each of the symmetric encryption schemes considered. Perhaps the best way to avoid these attacks is not by attempting to remove all potentially-damaging oracles, but rather to remove the adversary's ability to alter plaintext bits in the first place. One very-effective way to accomplish this is with authenticated encryption.
Security experts have long been recommending that encryption always be accompanied by authentication [Bel96]. Vaudenay and the present paper lend further support to this recommendation. If it were impossible for the adversary to produce valid ciphertexts other than those he has already seen, all attacks mentioned in this paper would vanish.
One might object to the assertion here that authentication is truly required; after all, we have shown methods in Section 4 which demonstrated that it is possible, with care, to remove the padding oracle altogether. And it is obviously possible to avoid implementing the length-revealing oracle mentioned in the previous section. However if we have learned anything through this exercise it is that side-channels like these are probably difficult to avoid when designing cryptographic protocols. It ``feels'' like the simple choice of how to pad a message before encryption would have absolutely zero impact on security, but as we have seen this is potentially untrue.
AUTHENTICATED ENCRYPTION. Each of the encryption schemes we have discussed meets the minimal security requirement for privacy: it is computationally infeasible to distinguish the encryption of a given message from the encryption of a random string of the same length. This is so-called ``semantic security'' under chosen-plaintext attack for an encryption scheme, usually abbreviated IND-CPA [BDJR97]. However, as we have seen, such a guarantee says nothing about the difficulty of producing new ciphertexts whose plaintexts are related to those already seen. A scheme which prevents this is called ``non-malleable'' [DDN00,BDPR98]. In particular, a non-malleable scheme does not allow one to flip bits in the ciphertext and induce flipped corresponding bits in the plaintext; therefore it is self-evident that our schemes do not meet this stronger notion of security.
It is disconcerting to see encryption primitives used as if they guarantee more than IND-CPA. A common example in protocols occurs when a party receives EK(x) and returns EK(x+1) to ``prove'' he holds the key K (here E() denotes some encryption scheme and x is a positive integer). Normal notions of security do not guarantee such properties. In fact, an adversary with no knowledge of K can easily produce EK(x+1) given EK(x) with many common instantiations of E. For example, if E is a stream cipher we can merely complement the least significant bit of EK(x) to produce EK(x+1) with probability about 0.5 (assuming that x is even with probability about 0.5 and that it is encoded as a string with its least-significant bit right-justified in the plaintext).
A notion of security strictly stronger than non-malleability is the following mouthful: integrity of ciphertexts with semantic security against chosen-plaintext attacks [BN00]. We will simply call this ``authenticated encryption.''
When we use authenticated encryption, we are guaranteed that (with overwhelming probability) an adversary will not be able to take a given ciphertext and manipulate it to produce a new valid ciphertext. Nor will he be able to combine two ciphertexts to produce a new valid ciphertext. In fact, the only valid ciphertexts he will be able to produce are (with overwhelming probability) repetitions of those he's seen generated as legitimate traffic. He will not be able to produce any new ones on his own. Authenticated encryption does provide the adversary with an oracle which returns VALID and INVALID for any ciphertexts he produces. However this oracle will (with overwhelming probability) return INVALID when given any ciphertext he has tampered with, thus rendering the side-channel attacks mentioned above (and indeed, any side-channel attacks which depend on ciphertext manipulation) ineffective.
COST OF AUTHENTICATED ENCRYPTION. There are several ways known for achieving authenticated encryption. Perhaps the most well-known is to encrypt the plaintext with any semantically secure scheme (like CBC Mode encryption), then apply a Message Authentication Code (MAC) to the resulting ciphertext. Assuming the MAC is ``strongly unforgeable,'' the resulting scheme will achieve authenticated encryption [BN00,KY00,Kra01]. How much additional cost is incurred by the authentication step? The fastest-known MACs can process messages of moderate length (say, 256 bytes) at around 10 cycles per byte [BCK96,BHK+99], so the additional cost is quite minimal. This approach also has the advantage of being free of patents.
Recently there have been several modes of operation which perform simultaneous encryption and authentication [Jut01,RBBK01,GD94]. Their performance is typically quite good; for example, OCB Mode [RBBK01] is about 6.5% slower than just CBC Mode encryption, and is fully parallelizable (whereas CBC Mode is not). It requires about half the cost of running CBC Mode encryption and CBC MAC (under the encrypt-then-MAC method above).
AND IT'S STILL POSSIBLE TO GO WRONG. The mere use of authenticated encryption does not guarantee that a particular implementation will avoid inducing side-channel oracles. We might leak information during the decryption and integrity check phases which would be useful to an adversary. In fact, Manger's attack on OAEP [Man01] was based on precisely this idea. There are doubtless analogous dangers on the symmetric side if one is not careful.
As a simple example, suppose on the sending side we pad then encrypt then MAC, but then on the receiving side we decrypt, strip the padding, and then check the MAC on the ciphertext last. Using this unusual ordering, we might send back an error message about invalid padding before checking to see if the ciphertext was authentic or not; this scheme would of course be vulnerable to the types of attacks exhibited in this paper. The message here is clear: check the authenticity first; if a received message is inauthentic, reject it without any further processing.
The cost of authenticated encryption is quite small and, when properly implemented, promises to eliminate a wide variety of side-channel attacks based on manipulation of ciphertexts. Authentication has long been thought of as a separate security goal, used only when one is concerned about such things as message integrity, authenticity of origin, and non-repudiation. It is often regarded as unnecessary in systems which require only privacy. But as we have seen, the ability to freely manipulate ciphertexts gives rise to a wide range of possible attacks based on side-channels which presumably cannot be exploited without this ability. These side-channels are demonstrably damaging and it is likely very difficult to avoid constructing them in real systems. In light of this, perhaps it is time to view authentication as a strongly-desirable property of any symmetric encryption scheme, including those where privacy is the only security goal.
The authors would like to thank Phil Rogaway for useful comments and suggestions, and Serge Vaudenay for providing us with an early draft of his paper. Kindest thanks to David Wagner for bringing our attention to additional related work. We would also like to thank the USENIX Security '02 program committee for their helpful comments.