Here is a diagram of a five-level game tree in which each of the two players has three available moves at each turn. The MAX player is trying to get the highest possible score; MIN is trying to hold MAX to the lowest possible score. The two players alternate two moves: MAX, then MIN, then MAX, then MIN. The bottom level (of 81 leaves) represents the value to MAX of each of the final game states.
Using just a straightforward minimax algorithm, label the values of the interior nodes of the tree.
(a) Assume that for each parent node, the children in the nodes are created and checked in left-to-right order as shown in the diagram. Show which of the 81 leaf nodes do not have to be checked if we use alpha-beta search.
(b) Do the same problem as (a), but this time assume that nodes are created and checked in right-to-left order.
Do problem 7.2 in the Russell-Norvig text.
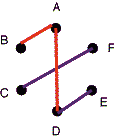
In class, we looked at the game of Sim. Just to recap: the game is played between two players, Red and Blue. (Red goes first.) The game board is a set of N points; in class, our value of N was 6, and the points were labeled A-F. Each player moves in turn by choosing an edge between two points; that edge is then marked in the player's color. The first player who creates a triangle in their own color is the loser. The figure below shows a sample 6-point game after each player has moved twice. The moves, in sequence, were:
RED A-B
If Red were (insanely) to choose B-D next, he would lose the game by forming the triangle ABD in red. Note, by the way, that edges are undirected: AB and BA are not counted as distinct moves.
Play a Sim game or two with a friend to familiarize yourself with the game.
How many distinct edges are there for a 6-point game? 7-point? 8-point? Give a general formula for an N-point game.
How many distinct triangles are there in a 6-point game? 7-point? 8-point? Give a general formula for an N-point game.
Briefly -- in a paragraph or so -- explain how the structure of a Sim-playing program would depend on the number of points in the starting game. (Compare, for example, the task of programming a Sim-player for a 100-point game with a Sim-player for a 6-point game.)
Write a program that plays Sim for a 6-point game against a human opponent. Your program should play a legal and plausible, but not necessarily expert, game. Include a listing of two games played between yourself and the program: one in which you play Red, the other in which you play Blue.